- #1
Wavefunction
- 99
- 4
Homework Statement
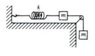
Two equal masses are constrained by the spring-and-pulley system shown in the accompanying
sketch. Assume a massless pulley and a frictionless surface. Let x be the extension of the
spring from its relaxed length. Derive the equations of motion by Lagrangian methods. Solve
for x as a function of time with the boundary conditions x = 0,\frac{dx}{dt} = 0 at t =0
Homework Equations
(1)\frac{∂L}{∂q_j}-\frac{d}{dt}\frac{∂L}{∂\dot{q_j}}+\sum_k λ_k(t)\frac{∂f_k}{∂q_j} = 0
The Attempt at a Solution
First I'll construct the Lagrangian L=T-U , T= \frac{m}{2}[\dot{x}^2+\dot{y}^2] , U = \frac{kx}{2}+mgy → L = \frac{m}{2}[\dot{x}^2+\dot{y}^2] - \frac{kx}{2}-mgy
Okay now, I also have the constraint that the total length of the string doesn't change. Also when I shift the x-coordinate in the positive direction the shift in the y-coordinate will be negative which implies:
dx=-dy → x = -y+C and let C=0 so that x+y = 0
Now, I have my constraint f(x,y) = 0 so now I can use (1) in order to find the equations of motion for the system:
(2) \frac{∂L}{∂x} = -kx, \frac{d}{dt}\frac{∂L}{∂\dot{x}} = \frac{d}{dt}[m\dot{x}] = m\ddot{x}, and λ\frac{∂f}{∂x} = λ
(3) \frac{∂L}{∂y} = -mg, \frac{d}{dt}\frac{∂L}{∂\dot{y}} = \frac{d}{dt}[m\dot{y}] = m\ddot{y}, and λ\frac{∂f}{∂y} = λ
Now, I simply add the corresponding pieces together:
(2') -kx-m\ddot{x}+λ = 0
(3') -mg-m\ddot{y}+λ = 0
From my constraint I can replace \ddot{y} with -\ddot{x} and add the two equations to solve for λ doing so gives:
(2')+(3'): -kx-mg+2λ = 0 → λ = \frac{kx+mg}{2}
Now that I have λ I can plug it into either (2') or (3') to solve for x I'll choose (2'):
-\frac{kx}{2} + \frac{mg}{2} - m\ddot{x} = 0 → \ddot{x}+\frac{k}{2m}x = \frac{g}{2}
I'll define ω\equiv \sqrt{\frac{k}{2m}} so that now the above DE is of the form of a simple harmonic oscillator with a constant driving force:
x(t)= x_c(t) + x_p(t), x_c(t) = Acos(ωt)+Bsin(ωt), and x_p(t) = C
\ddot{x_p}+ω^2x_p = \frac{g}{2} → C=\frac{g}{2ω^2} = \frac{gm}{k}
Then x(t) = Acos(ωt)+Bsin(ωt)+ \frac{gm}{k}
Now apply the boundary conditions:
0 = A+\frac{gm}{k}
\dot{x} = -Aωsin(ωt)+Bωcos(ωt) → 0=Bω → x(t)=-\frac{gm}{k}cos(ωt)+\frac{gm}{k}
Finally, x(t) = \frac{gm}{k}[1-cos(\sqrt{\frac{k}{2m}}t)] and of course y(t) = -x(t) so
y(t) = -\frac{gm}{k}[1-cos(\sqrt{\frac{k}{2m}}t)]
So I'm fairly certain I got this correct (but it never hurts to check!) I'm fairly certain because my forces of constraint are the same for both coordinates (i.e tension in the string is the same everywhere) Also I ended up having only one canonical coordinate which corresponds to one dof : s=Dn-m where s is the number of degrees of freedom, D is the number of dimensions each particle is allowed to move in, n is the number of particles, and m is the number of constraints on the coordinate(s). Using this relation: s=(1)(2)-(1)=1 which is exactly the number of coordinates I ended up with at the end. Thank you in advance for looking over my work. (:
