Solving Gas Work: Va, Vb, Pa, Pb

[perplexabot]

Hi all. Trying to find work done for a gas... Here is the question:

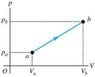
A quantity of air is taken from state a to state b along a path that is a straight line in the pv-diagram (figure is attached). If Va = 0.07, Vb = .11, Pa = 100,000 , Pb = 140,000. What is the work W done by the gas in this process? Assume that the gas may be treated as ideal.

Ok i know the area under the graph is work. But instead of doing it that way can i use this way?:
W = (integral of) p dV
and since p is changing linearly: p = mV + b where b = 0 and m = (Pb - Pa)/(Vb - Va) = k
so p = k* V

substituting that back into the Work equation i get:
W = (integral of) k * V dV
=> W = k * (integral of ) V dV
=> W = k/2 (Vb² - Va²)

ok so after all this i end up with 3600 J which is wrong (actual answer is 4800). Can any1 tell me what I'm doing wrong? or why this technique doesn't work?

once again i know u can just find the area of the graph, but i want to know why this way is wrong..
Thanks all.

 

[Philip Wood]

Where has "So p = k.V" come from? It implies that the line goes through the origin, which it doesn't. I think something has gone wrong with your algebra, though this started correctly.

 

[perplexabot]

Where has "So p = k.V" come from? It implies that the line goes through the origin, which it doesn't. I think something has gone wrong with your algebra, though this started correctly.

p = k * V where k is just m or the slope ( (Pb - Pa)/(Vb - Va) ).
and if the figure is scaled correctly, if you continue the line, it will pass through the origin.

could it be that i didn't take into account the integrating constant?

 

[Philip Wood]

I don't think the line does go through the origin. PA/VA doesn't equal PB/VB.

 

[sophiecentaur]

could it be that i didn't take into account the integrating constant?

With a definite integral there isn't and "integrating constant" is there? The difference between values at the limits will cancel it out.

Are you sure that the "actual answer" is correct? I can't be bothered to do the substitution sums but your algebra looks fine. If you have put the right numbers into the result of your algebra / integration, then your answer should be right, I think.

I think your way of working out the area is using the 'wrong' trapesium. If you use the one with the p along the base, you get the same answer as your integration method. (i.e. swap your axes)

I must say, I started off thinking Boyle's Law and got totally confused until I re-read the OP!

 

[Philip Wood]

To reiterate: the linear relationship between P and V cannot be written as P = kV, for the reason I've given. This needs sorting out before proceeding to the integration.

 

[perplexabot]

To reiterate: the linear relationship between P and V cannot be written as P = kV, for the reason I've given. This needs sorting out before proceeding to the integration.

hey... alright so your saying p =mV + b where b is NOT equal to zero because the line does NOT pass though the origin...

p_a = m*V_a + b
p_a = 100,000
V_a = .07
m = (p_b - p_a) / (V_b - V_a) = (140,000 - 100,000)/(.11 - .07)
= 40,000/.04 = 1 *10⁶

b = p_a - m*V_a = 100,000 - (10⁶ * .07) = 30,000

so p = kV + b
=> p = 10⁶V + 30,000

using the above equation for p, I subbed it back into the Work equation and solved... I got exactly 4800 (which is the correct answer). So as you said Philip, the line does NOT pass through the origin.. Thanks for your help...

 

[Philip Wood]

Well done for your persistence! I expect, though, that having satisfied yourself that the integration method works, you'll use the simple 'area of trapezium' method if you meet straight lines again in the p, V context!

 

[perplexabot]

With a definite integral there isn't and "integrating constant" is there? The difference between values at the limits will cancel it out.

Are you sure that the "actual answer" is correct? I can't be bothered to do the substitution sums but your algebra looks fine. If you have put the right numbers into the result of your algebra / integration, then your answer should be right, I think.

I think your way of working out the area is using the 'wrong' trapesium. If you use the one with the p along the base, you get the same answer as your integration method. (i.e. swap your axes)

I must say, I started off thinking Boyle's Law and got totally confused until I re-read the OP!

ok thanks for clearing that out. i didn't know that only indefinite integrals had integrating constants. that actually helps a lot. thanks

 

[perplexabot]

Well done for your persistence! I expect, though, that having satisfied yourself that the integration method works, you'll use the simple 'area of trapezium' method if you meet straight lines again in the p, V context!

yes, i will be using the area method from now on. i just wanted to see if i can do it otherwise.. thanks for the help...

 

[sophiecentaur]

To reiterate: the linear relationship between P and V cannot be written as P = kV, for the reason I've given. This needs sorting out before proceeding to the integration.

I think that you, as I did at first, have missed the point and not read the question fully. You can make p proportional to v if you like over a limited range. Boyle's Law (pv=a constant) only holds for constant temperature. You can ' insist' on any relationship as long as you are prepared to add or take away the appropriate amount of internal energy.
That graph could not ever go to the origin - it wouldn't hold to a straight line without ridiculous / impossible imposed conditions.

 

[sophiecentaur]

yes, i will be using the area method from now on. i just wanted to see if i can do it otherwise.. thanks for the help...

Yes but you need to choose the right area;one that integrates p dv and not v dp. In the same way that Work done = distance moved times force and not force change times distance.

 

[Philip Wood]

I think that who missed the point and who didn't is clear from the sequence of responses.