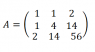I would have not bothered at all to get the eigenvalues; I would just perform Cholesky factorization on A: find an upper-triangular matrix U such that A = U^T * U. Just expand this out to find the following algorithm for U:
U[1,1] = sqrt(A[1,1]) and for j=2,...,n, U[1,j] = A[1,j]/U[1,1].
for i from 2 to n do U[i,i]=sqrt(A[i,i]-sum_{k=1..i-1} U[k,i]^2) and for j=i+1,...,n,
U[i,j] = (A[i,j] - sum_{k=1..i-1} U[k,i]*U[k,j])/U[i,i].
(Note: even if you have not seen this before, it only takes about 5-10 minutes to master, and then you can do it quickly by hand for matrices up to about 10x10 or even a bit more, using nothing beyond a hand-held calculator.)
For your matrix A we have U = [[1,1,2],[0,sqrt(3),4sqrt(3)],[0,0,2]] (= [row1,row2,row3])
So, if u1 = (row1 of U) * <x,y,z> = x+y+2z, u2 = (row2 of U) * <x,y,z> = sqrt(3)y + 4sqrt(3)z and u3 = (row3 of U) * <x,y,z> = 2z, then Q = x^T A x = u1^2 + u2^2 + u3^2. If you expand this out you will see that you get back to your original form, so it gives you exactly what you want: Q written as a sum of squares. No eigenvalues need be involved at all.
RGV