Solving Momentum Problem: Find Speed of Package & Cart

  • Thread starter Thread starter makeAwish
  • Start date Start date
  • Tags Tags
    Momentum Urgent
AI Thread Summary
In a physics problem involving a cart and a package, the speed of the package just before landing in the cart is calculated to be 9.23 m/s, using the principle of conservation of energy, despite initial confusion about the angle of the chute. The final speed of the cart after the package lands is determined to be 4.26 m/s, with momentum conservation applied in the horizontal direction. The discussion emphasizes the importance of considering both horizontal and vertical components of velocity when calculating momentum. Additionally, it highlights that signs in velocity calculations are crucial for obtaining accurate results. Understanding these principles is essential for solving similar momentum problems effectively.
makeAwish
Messages
128
Reaction score
0
Homework Statement

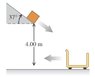
In a shipping company distribution center, an open cart of mass 51.0kg is rolling to the left at a speed of 5.50m/s (see the figure). You can ignore friction between the cart and the floor. A 10.0kg package slides down a chute that is inclined at 37degrees from the horizontal and leaves the end of the chute with a speed of 2.60m/s . The package lands in the cart and they roll off together.



(a) If the lower end of the chute is a vertical distance of 4.00 above the bottom of the cart, what is the speed of the package just before it lands in the cart?
ans: 9.23m/s

(b) What is the final speed of the cart?
ans: 4.26m/s


The attempt at a solution

I think this is a prefectly inelastic collision when the package falls into the cart.
For first part, is it use v^2 = u^2 + 2as?
where u = 2.6m/s and a = -9.8 and s = -4?
i get the answer 9.23, but i not sure if this is correct cos i din take into acct that the package falls from a slope at an angle. does the angle matter?


For 2nd part, i duno how to do. I tried using conservation of momentum but i can't get the answer.
my eqn is: Mp * Vpi + McVci = (Mp + Mc)Vf
and i get Vf as 5.02m/s

Pls help me.. Thanks!
 

Attachments

  • YF-08-46.jpg
    YF-08-46.jpg
    5.1 KB · Views: 617
Physics news on Phys.org
janettaywx said:
I think this is a prefectly inelastic collision when the package falls into the cart.
For first part, is it use v^2 = u^2 + 2as?
where u = 2.6m/s and a = -9.8 and s = -4?
i get the answer 9.23, but i not sure if this is correct cos i din take into acct that the package falls from a slope at an angle. does the angle matter?
Your thinking is probably a bit off, but lucky for you you get the right answer anyway. To do it right, using acceleration, you'd need the component of the initial velocity in the vertical direction. But then you'd be adding back the horizontal component later to find the total velocity.

Even better would be to use conservation of energy. Then it would be clear that the angle doesn't matter (for this part).

For 2nd part, i duno how to do. I tried using conservation of momentum but i can't get the answer.
my eqn is: Mp * Vpi + McVci = (Mp + Mc)Vf
and i get Vf as 5.02m/s
Hint: During the collision of package and cart, momentum (a vector) is only conserved in one direction. (Which direction?)
 
Doc Al said:
Your thinking is probably a bit off, but lucky for you you get the right answer anyway. To do it right, using acceleration, you'd need the component of the initial velocity in the vertical direction. But then you'd be adding back the horizontal component later to find the total velocity.

Even better would be to use conservation of energy. Then it would be clear that the angle doesn't matter (for this part).


Hint: During the collision of package and cart, momentum (a vector) is only conserved in one direction. (Which direction?)

oh.. we need to add back the horizontal part! it din occur to me that we need to add that back. hmm. how do we know if we can use energy to solve a qns?
 
during collision, momentum is conserved in x direction?
 
Last edited:
janettaywx said:
during collision, momentum is conserved in x direction?

Yes.
 
janettaywx said:
how do we know if we can use energy to solve a qns?
Just try it and see! In this case, mechanical energy is conserved (in part A) so it can be used.

janettaywx said:
during collision, momentum is conserved in x direction?
Right! Now you need the speed of the package in that direction to analyze the collision.
 
so its Mp*Vpxi + Mc*Vcxi = (Mc + Mp)*Vxf right?

i get 4.94m/s, but answer is 4.26m/s..
 
janettaywx said:
so its Mp*Vpxi + Mc*Vcxi = (Mc + Mp)*Vxf right?
Right.
i get 4.94m/s, but answer is 4.26m/s..
What were your values for Vpxi & Vcxi?
 
my Vpxi is 2.6cos 37
Vcxi is 5.5

correct?
 
  • #10
janettaywx said:
my Vpxi is 2.6cos 37
Vcxi is 5.5
Correct. Different signs, of course.

Recheck your arithmetic: 2.6 cos 37 = ?
 
  • #11
we must include the signs?? means vcxi is -5.5??
2.6cos 37 is 2.0764
 
  • #12
means even for momentum qns, we need to consider the signs for velocity?

can i ask sth? like when we calculating potential energy, the gravt acceleration, do we need to consider the -ve sign if we take upward as positive?
 
  • #13
janettaywx said:
we must include the signs?? means vcxi is -5.5??
2.6cos 37 is 2.0764

Absolutely. Signs matter.

And that's the difference in your answer that you are looking for.
 

Similar threads

Solve Momentum Problem: Find Bullets/Sec Needed for Cart to Reach 19m/s
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top