Solving Pulley Systems with Multiple Masses and Angles

[mburt]

Homework Statement

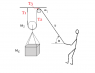
A crate is pulled up using frictionless pulleys in the manner shown in the figure. The angle is 45 degrees. The masses are, for the small pulley, m₁=3.5 kg, for the traveling pulley, M₂=6.5 kg, and for the crate, M_C=44.2 kg. What is the minimum tension with which the operator must pull on the cable (assume the cable is of negligible mass) in order to slowly raise the crate.

(See the attached picture below)

Homework Equations

First of all note that in the diagram attached, the BLACK parts are the original question, and the RED parts are things I added to help in solving it.

1) I know that T₃ has to support at least m₁. How would I figure out how much of M₂ and M_C it supports?

2) Does the Y component of T (ie. Tsin45) equal T₂ in the diagram?

3) Since the problem says "slowly raise", does this mean that net force in the Y-direction is zero?

The Attempt at a Solution

Well I drew FBDs at m₁, and M₂ and ended up with these statements:

At m₁:

T₃ + Tsin45 - T₂ - m₁g = 0

At M₂:

T₁ + T₂ - M₂g - M_Cg = 0

But seeings there's only 2 equations and 4 unknowns it seems unsolvable.

There must be SOME relationship between T, T₁, T₂, and T₃ that I'm not seeing.

Thanks in advance,

Mike

 

[cheahchungyin]

In this situation, since all the tensions are from the same string, T1=T2=T3=T

 

[mburt]

Wow really? Are you sure it's that simple?

 

[cheahchungyin]

Its the same string without any node. any pull on the other side will affect the whole string right?

 

[mburt]

Ok that seems like it makes sense...one more question though.. how would the pulley with mass = m₁ affect the system? Since it's attached to the ceiling wouldn't it's weight be canceled out by T₃?

 

[cheahchungyin]

m1 won't take any account unless it has friction.

 

[mburt]

Alright thanks, I'll try to solve this again now. I appreciate your help

 

[mburt]

I got an answer of T = 351.7N but unfortunately that's not right.I came up with the statement:

T₁ + T₂ - M₂ - M_C = 0

Where T₁ and T₂ = Tsin45

So:

2Tsin45 = 497.367N

and T = 351.7N

But this isn't the right answer... Thanks again for your help!

 

[cheahchungyin]

Do you have the answer sheet? what's the correct answer?

 

[mburt]

I don't have the answer sheet, but its an online assignment and when I enter an answer It tells me if its wrong.

The only thing I can figure is that the tension on the left side of the larger pulley is different than the tension on the right side of that pulley

 

[cheahchungyin]

hmmm... did I miss something... >.<
try 248.7

 

[cheahchungyin]

Okay sorry for being not able to help. got a little confused

 

[mburt]

No don't say sorry, I appreciate your help!

I only have two tries left so I might try to work it out again...maybe i'll get some more understanding about this question

 

[mburt]

248.7N was the correct answer...so thanks!

I guess no matter what the angle T is at it will always be equal to the tension on the other side of the pulley

 

[cheahchungyin]

Oh haha!
The problem is I didn't know what's the purpose of the angle, so I got confused lol.
Thanks too that I learned something here :D