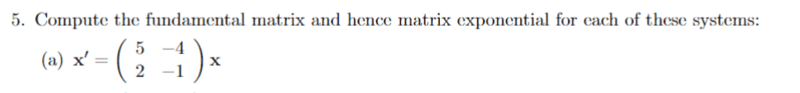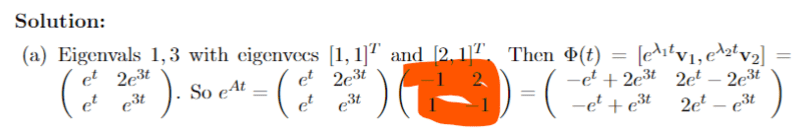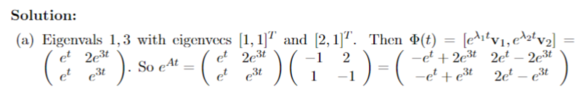SUMMARY
The discussion focuses on solving systems of differential equations using the matrix exponential method, specifically through the transformation of the matrix A into its Jordan normal form. The transformation is essential for computing the state transition matrix, denoted as eAt. The eigenvector matrix H, defined as H = [[1, 2], [1, 1]], plays a crucial role in this process, and understanding its inverse H-1 is necessary for reverting to the original basis. Additionally, the fundamental matrix Φ is discussed in relation to the equation Φ'(t) = eAtΦ(0).
PREREQUISITES
- Matrix exponentiation techniques
- Understanding of Jordan normal form
- Knowledge of eigenvalues and eigenvectors
- Familiarity with fundamental matrices in differential equations
NEXT STEPS
- Study the process of transforming matrices to Jordan normal form
- Learn how to compute the inverse of a matrix, specifically for eigenvector matrices
- Explore the derivation and application of the state transition matrix eAt
- Investigate the properties and applications of fundamental matrices in solving differential equations
USEFUL FOR
Mathematicians, engineers, and students in applied mathematics or control theory who are solving systems of differential equations and require a deeper understanding of matrix methods.