trini
- 216
- 1
ok, so here's the problem:
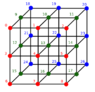
given a 3 x 3 x 3 cubic system of vertices, a starting vertex, and an end vertex, how many paths that pass through all vertices ONLY ONCE and start and end at the given vertices(for example let's say the starting and end vertices are two opposite corner vertices) can be formed? rules:
a)a vertex may only be passed through once
b) all vertices(in this case 27) must be passed
c)all motions are in the x, y, or z direction only(ie, diagonal vertices not connected) eg:
D----------E
| ..C
| ./
| /
A----------B
so if A is the starting vertex(a corner) it can then only go to B,C or D(not E as it is not immediately adjacent)[ps ignore the full stops by the path going to C, they are just there for spacing)
given a 3 x 3 x 3 cubic system of vertices, a starting vertex, and an end vertex, how many paths that pass through all vertices ONLY ONCE and start and end at the given vertices(for example let's say the starting and end vertices are two opposite corner vertices) can be formed? rules:
a)a vertex may only be passed through once
b) all vertices(in this case 27) must be passed
c)all motions are in the x, y, or z direction only(ie, diagonal vertices not connected) eg:
D----------E
| ..C
| ./
| /
A----------B
so if A is the starting vertex(a corner) it can then only go to B,C or D(not E as it is not immediately adjacent)[ps ignore the full stops by the path going to C, they are just there for spacing)
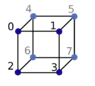
 , you are right. I forgot the edge from vertex 7 to vertex 4.
, you are right. I forgot the edge from vertex 7 to vertex 4.