Solving the differential equation of planetary motion

[RpWinter]

Hey, this is how i tried solving the differential equation

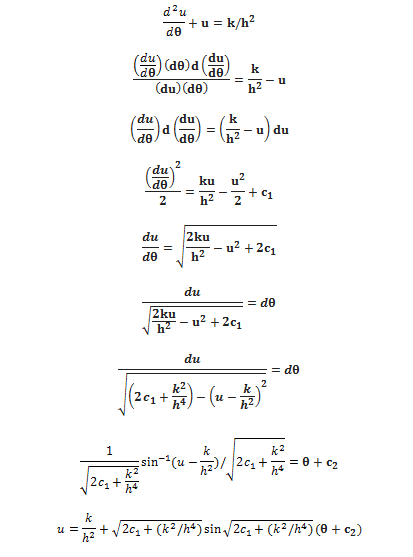
The solution however does not match the general solution of the equation. Also differentiating it twice does not give me the previous equation. Please tell me if i did some mistake while solving.
I already know how to solve by finding CF and PI. I want to know what's wrong with this method.

 

[dRic2]

http://gsjournal.net/Science-Journals/Research Papers-Astrophysics/Download/3763

 

[RpWinter]

http://gsjournal.net/Science-Journals/Research Papers-Astrophysics/Download/3763

I have already seen this derivation. Here the differential equation is solved by finding Central function and Particular Integral of the Differential equation. I want to know what's wrong with the method that i have used. Both of them are not giving the same result.

 

[dRic2]

Sorry I don't understand your equations or where they came from. I thought you were looking for a simpler solution