- 2,180
- 2,690
I want to solve the heat equation numerically. The equation is: $$k \dfrac{\partial^2 T}{\partial x^2} = \dfrac{\partial T}{\partial t}.$$ This is a parabolic PDE.
Following this pdf (specifically, equation 7 given on page 3), I wrote the following Python function to implement the explicit algorithm:
Our college Professor gave us a sample problem to test our programs. The given values are as follows:
And I get this graph:
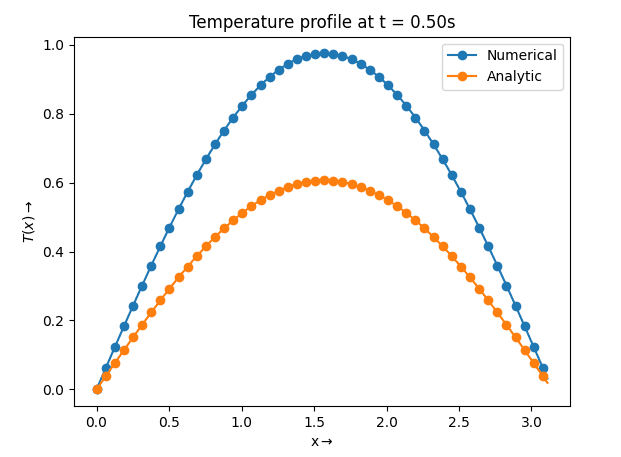
Obviously, the numerical solution doesn't match the analytic solution.
I double-checked my function, and there seems to be no error. But there is an error somewhere, right?
If I print
Ignore the
Any idea where the problem is occurring?
Following this pdf (specifically, equation 7 given on page 3), I wrote the following Python function to implement the explicit algorithm:
Python:
import numpy as np
def heat_equation_explicit(t0, t_end, dt, dx, k, initial_profile):
"""
Solves the heat equation using explicit algorithm.
Parameters
----------
t0 : float
The start of time.
t_end : float
The end of time.
dt : float
Time step.
dx : float
Step size on x-axis.
k : float
Diffusivity.
initial_profile : numpy.ndarray
The initial heat profile for all values of x over which the solution has to be calculated,
(i.e. T(x, 0) ∀ x ∈ np.arange(x0, x_end, dx)). The first and the last elements should be the
boundary values, i.e. T(x0, t) and T(x_end, t), which will remain constant with time.
Returns
-------
numpy.ndarray
The heat profile at t = t_end.
"""
# Number of steps:
num_t = round((t_end - t0) / dt)
num_x = np.size(initial_profile)
old_profile = initial_profile
global finalProfile_numerical
lamb = (k * dt) / (dx ** 2)
for j in range(0, num_t):
# Initialise the variable:
finalProfile_numerical = np.zeros(num_x)
# Keep the boundary values at the two ends:
finalProfile_numerical[0] = initial_profile[0]
finalProfile_numerical[-1] = initial_profile[-1]
# Compute the new profile:
for i in range(1, num_x - 1):
u_old_iPlus1 = old_profile[i + 1]
u_old_iMinus1 = old_profile[i - 1]
finalProfile_numerical[i] = old_profile[i] + lamb * (u_old_iPlus1 - 2 * old_profile[i] + u_old_iMinus1)
old_profile = finalProfile_numerical
return finalProfile_numerical- ##x \in [0, \pi]##
- ##T(0, t) = T(\pi,t) = 0##
- ##T(x,0) = \sin x##
- ##k = 0.05##
- Analytical solution: ##T(x,t) = \exp(-t) \sin x##
- I have to compute the final profile at ##t = 0.5s.##
Python:
import math
import numpy as np
import matplotlib.pyplot as plt
x0 = 0
xEnd = math.pi
dx = math.pi / 100
t0 = 0
tEnd = 0.5
dt = 0.01
k = 0.05
xVal = np.arange(x0, xEnd, dx)
# Values of T(x, 0) at all x. Includes T(x0, t) at the beginning, and T(x_end, t) at the end.
initialProfile = np.sin(xVal)
finalProfile_numerical = heat_equation_explicit(t0, tEnd, dt, dx, k, initialProfile)
finalProfile_analytic = math.exp(-0.5) * np.sin(xVal)
# Plot the numerical solution:
plt.plot(xVal, finalProfile_numerical, '-o', label="Numerical", markevery=2)
# Plot the analytical solution:
plt.plot(xVal, finalProfile_analytic, '-o', label='Analytic', markevery=2)
plt.xlabel(r'x$\rightarrow$')
plt.ylabel(r'$T(x)\rightarrow$')
plt.title("Temperature profile at t = " + f'{tEnd:.2f}' + "s")
plt.legend(loc='best')
plt.show()Obviously, the numerical solution doesn't match the analytic solution.
I double-checked my function, and there seems to be no error. But there is an error somewhere, right?
If I print
final_profile_numerical / final_profile_analytic, I get:
Code:
[ nan 1.60800745 1.60800745 1.60800745 1.60800745 1.60800745
1.60800745 1.60800745 1.60800745 1.60800745 1.60800745 1.60800745
1.60800745 1.60800745 1.60800745 1.60800745 1.60800745 1.60800745
1.60800745 1.60800745 1.60800745 1.60800745 1.60800745 1.60800745
1.60800745 1.60800745 1.60800745 1.60800745 1.60800745 1.60800745
1.60800745 1.60800745 1.60800745 1.60800745 1.60800745 1.60800745
1.60800745 1.60800745 1.60800745 1.60800745 1.60800745 1.60800745
1.60800745 1.60800745 1.60800745 1.60800745 1.60800745 1.60800745
1.60800745 1.60800745 1.60800745 1.60800745 1.60800745 1.60800745
1.60800745 1.60800745 1.60800745 1.60800745 1.60800745 1.60800745
1.60800745 1.60800745 1.60800745 1.60800745 1.60800745 1.60800745
1.60800745 1.60800745 1.60800745 1.60800745 1.60800746 1.60800746
1.60800747 1.60800748 1.60800752 1.60800757 1.60800769 1.60800788
1.60800825 1.60800886 1.60800999 1.60801179 1.60801496 1.60801993
1.6080283 1.60804126 1.60806232 1.60809452 1.60814542 1.60822265
1.60834263 1.60852485 1.60880718 1.60924297 1.60993333 1.61105178
1.61296191 1.61650076 1.6242027 1.64872127]nan in the front. Interestingly, note that ##1 / \exp(-0.5) = 1.648##.Any idea where the problem is occurring?