Trafi
- 5
- 2
- TL;DR
- Methods to solve operating point of transformer with nonlinear B-H curve and possibly an air gap
What are the possible ways of solving the operating point of air gapped transformer with nonlinear B-H curve? For example let's consider 3C90 E34 sized core with 0.5 mm airgap. I know that the magnetomotive force over the ferrite part can be formulated as function of the reluctances: ##F_{m,ferrite} = F_{m,tot} * R_{ferrite}/(R_{ferrite}+R_a)##, where ##R_{ferrite}## is the reluctance of the ferrite part and ##R_a## is the reluctance of the air gap. The problem that I do not know how to solve is the fact the ##R_{ferrite}## is also a nonlinear function of the ##F_{m,ferrite}##. I guess this calls for some sort of iterative solution. The only solution method I could think of would be to make piecewise linear approximation from the table of permeability vs Fm and make a guess about the operating point, calculate the ##R_{ferrite}(B)##, recalculate ##F_{m,ferrite}## and do this in a loop until the solution converges.
However, there is another problem. The datasheets does not give the the permeability as a function of field intensity but only as a function of something called peak flux density as show in the attached picture. I could of course turn the reluctance and magnetomotive force into flux but I guess that for my solution I would need the permeability of a small ac excitation on top of a large dc offset. I do not know if that is the case but amplitude permeability as a function of peak flux density sounds to me like it would be the average permeability over large signal sine wave excitation with peak value shown in the X-axis. If this is the case would I need to solve the permeability as a function of field intensity by differentiating the B-H curve?
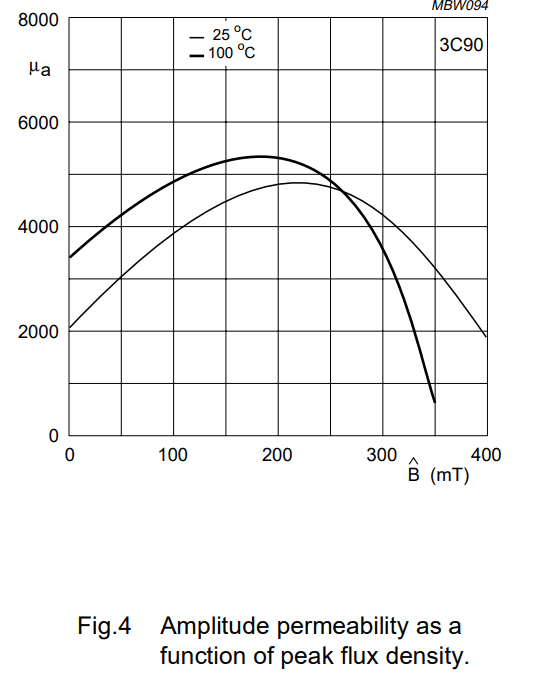
What are the standard ways to solve these type of equations and how could one solve the flux of a real transformer as a function of MMF using the datasheet of the ferrite core? Also making the piecewise linear approximation by hand seems like quite laborious task and I wonder if there are some tools available for these kind of situations for example in octave or as python library. Maybe instead of piecewise linear approximation some sort of curve fitting would be better? Also I want to emphasize that I am especially interested in the nonlinear region near saturation so just approximating the curve with single linear straight curve is not adequate.
ETD34 3C90 datasheet: http://www.farnell.com/datasheets/1468408.pdf
3C90 material datasheet: https://elnamagnetics.com/wp-conten...ube-Materials/3C90_Material_Specification.pdf
However, there is another problem. The datasheets does not give the the permeability as a function of field intensity but only as a function of something called peak flux density as show in the attached picture. I could of course turn the reluctance and magnetomotive force into flux but I guess that for my solution I would need the permeability of a small ac excitation on top of a large dc offset. I do not know if that is the case but amplitude permeability as a function of peak flux density sounds to me like it would be the average permeability over large signal sine wave excitation with peak value shown in the X-axis. If this is the case would I need to solve the permeability as a function of field intensity by differentiating the B-H curve?
What are the standard ways to solve these type of equations and how could one solve the flux of a real transformer as a function of MMF using the datasheet of the ferrite core? Also making the piecewise linear approximation by hand seems like quite laborious task and I wonder if there are some tools available for these kind of situations for example in octave or as python library. Maybe instead of piecewise linear approximation some sort of curve fitting would be better? Also I want to emphasize that I am especially interested in the nonlinear region near saturation so just approximating the curve with single linear straight curve is not adequate.
ETD34 3C90 datasheet: http://www.farnell.com/datasheets/1468408.pdf
3C90 material datasheet: https://elnamagnetics.com/wp-conten...ube-Materials/3C90_Material_Specification.pdf
Last edited: