Math Challenge - September 2019

[fresh_42]

Questions

1. Consider the ring $R= C([0,1], \mathbb{R})$ of continuous functions $[0,1]\to \mathbb{R}$ with pointwise addition and multiplication of functions. Set $M_c:=\{f \in R\mid f(c)=0\}$.

(a) (solved by @mathwonk ) Show that the map $c \mapsto M_c, c \in [0,1]$ is a bijection between the interval $[0,1]$ and the maximal ideals of $R$.

(b) Show that the ideal $M_c$ is not finitely generated.

Hint: Assume not and take a generating set $\{f_1, \dots, f_n\}$. Consider the function $f = |f_1| + \dots + |f_n|$ and play with the function $\sqrt{f}$ to obtain a contradiction.


2. We all know that the geometric mean is less than the arithmetic mean. I memorize it with $3\cdot 5 < 4\cdot 4$. Now we consider the arithmetic-geometric mean $M(a,b)$ between the two others. Let $a,b$ be two nonnegative real numbers. We set $a_0=a\, , \,b_0=b$ and define the sequences $(a_k)\, , \,(b_k)$ by
$$
a_{k+1} :=\dfrac{a_k+b_k}{2}\, , \,b_{k+1}=\sqrt{a_kb_k}\quad k=0,1,\ldots
$$
Then the arithmetic-geometric mean $M(a,b)$ is the common limit
$$
\lim_{n \to \infty}a_n = M(a,b) = \lim_{n \to \infty}b_n
$$
It is not hard to show that both sequences converge and that their limit is the same by using the known inequality and the monotony of the sequences.

Prove that for positive $a,b\in \mathbb{R}$ holds
$$
T(a,b):=\dfrac{2}{\pi} \int_0^{\pi/2}\dfrac{d\varphi}{\sqrt{a^2\cos^2 \varphi +b^2 \sin^2 \varphi }} = \dfrac{1}{M(a,b)}
$$


3. (solved by @StoneTemplePython ) If $A,B,C,D$ are four points in the plane, show that
$$
\operatorname{det} \begin{bmatrix}
0&1&1&1&1 \\ 1&0&|AB|^2&|AC|^2&|AD|^2 \\ 1&|AB|^2&0&|BC|^2&|BD|^2 \\ 1&|AC|^2&|BC|^2&0&|CD|^2 \\ 1&|AD|^2&|BD|^2&|CD|^2&0
\end{bmatrix} = 0
$$


4. Let $T \in \mathcal{B}(\mathcal{H}_1,\mathcal{H}_2)$ a linear, continuous (= bounded) operator on Hilbert spaces.
Prove that the following are equivalent:
(a) $T$ is invertible.
(b) There exists a constant $\alpha > 0$, such that $T^*T\geq \alpha I_{\mathcal{H}_1}$ and $TT^*\geq \alpha I_{\mathcal{H}_2}\,.$ $A \geq B$ means $\langle (A-B)\xi\, , \,\xi \rangle \geq 0$ for all $\xi\,.$


5. Let $a,b \in \mathbb{F}$ be non-zero elements in a field of characteristic not two. Let $A$ be the four dimensional $\mathbb{F}-$space with basis $\{\,1,\mathbf{i},\mathbf{j},\mathbf{k}\,\}$ and the bilinear and associative multiplication defined by the conditions that $1$ is a unity element and
$$
\mathbf{i}^2=a\, , \,\mathbf{j}^2=b\, , \,\mathbf{ij}=-\mathbf{ji}=\mathbf{k}\,.
$$
Then $A=\left( \dfrac{a,b}{\mathbb{F}} \right)$ is called a (generalized) quaternion algebra over $\mathbb{F}$.
Show that $A$ is a simple algebra whose center is $\mathbb{F}$.


6. Prove that the quaternion algebra $\left( \dfrac{a,1}{\mathbb{F}} \right)\cong \mathbb{M}(2,\mathbb{F})$ is isomorphic to the matrix algebra of $2\times 2$ matrices for every $a\in \mathbb{F}-\{\,0\,\}\,.$


7. (solved by @Not anonymous ) Show that there are infinitely many primes of the form $4k+3\, , \,k\in \mathbb{N}_0$.


8. (solved by @benorin ) Do $\displaystyle{\sum_{n=0}^\infty}\, \dfrac{(-1)^n}{\sqrt{n+1}}$ and the Cauchy product $\left( \displaystyle{\sum_{n=0}^\infty}\, \dfrac{(-1)^n}{\sqrt{n+1}} \right)^2$ converge or diverge?


9. (solved by @DEvens ) Consider the curve $\gamma\, : \,\mathbb{R}\longmapsto \mathbb{C}\, , \,\gamma(t)=\cos(\pi t)\cdot e^{\pi i t}\,.$

(a) Find the minimal period of $\gamma$,

(b) prove that $\gamma(\mathbb{R})\equiv\{\,(x,y)\in \mathbb{R}^2\,|\,x^2+y^2-x=0\,\}$,

(c) show that $\gamma(\mathbb{R})$ is symmetric to the $x-$axis,

(d) parameterize $\gamma$ with respect to its arc length.


10. (solved by @DEvens ) Let $\gamma\, : \,I \longrightarrow \mathbb{R}^n$ be a regular curve with unit tangent vector $T=\dfrac{d}{dt} \gamma\,.$ A (orthonormal) frame is a (smooth) $C^\infty-$ transformation $F\, : \,I \longrightarrow \operatorname{SO}(n)$ with $F(t)e_1=T(t)$ where $\{\,e_i\,\}$ is the standard basis of $\mathbb{R}^n\,.$ The pair $(\gamma,F)$ is called a framed curve, and the matrix $A$ given by $\dfrac{d}{dt}F=F'=FA$ is called derivation matrix of $F$.

Let $F_0\, : \,\mathbb{R}\longrightarrow \operatorname{SO}(n)$ be a frame of a regular curve $\gamma\, : \,\mathbb{R}\longrightarrow \mathbb{R}^n$. Show that

(a) If $F\, : \,\mathbb{R}\longrightarrow \operatorname{SO}(n)$ is another frame of $\gamma$, then there exists a transformation $\Phi\, : \,\mathbb{R}\longrightarrow \operatorname{SO}(n)$ with $\Phi(t)e_1=e_1$ for all $t\in \mathbb{R}$ and $F=F_0\Phi\,.$

(b) If on the other hand $\Phi\, : \,\mathbb{R}\longrightarrow \operatorname{SO}(n)$ is a smooth transformation with $\Phi(t)e_1=e_1\,,$ then $F:=F_0\cdot\Phi$ defines a new frame of $\gamma$.

(c) If $A_0$ is the derivation matrix of $F_0$, and $A$ the derivation matrix of the transformed frame $F:=F_0\Phi$ with $\Phi$ as above, then
$$
A=\Phi^{-1}A_0\Phi +\Phi^{-1}\Phi'
$$

11. (solved by @Not anonymous ) Show that the number of ways to express a positive integer $n$ as the sum of consecutive positive integers is equal to the number of odd factors of $n$.


12. (solved by @Not anonymous ) How many solutions in non-negative integers are there to the equation:
$$
x_1+x_2+x_3+x_4+x_5+x_6=32
$$


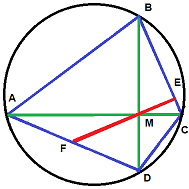
13. (solved by @etotheipi ) Let $A, B, C$ and $D$ be four points on a circle such that the lines $AC$ and $BD$ are perpendicular. Denote the intersection of $AC$ and $BD$ by $M$. Drop the perpendicular from $M$ to the line $BC$, calling the intersection $E$. Let $F$ be the intersection of the line $EM$ and the edge $AD$. Then $F$ is the midpoint of $AD$.

14. (solved by @timetraveller123 ) Prove that every non negative natural number $n\in \mathbb{N}_0$ can be written as
$$
n=\dfrac{(x+y)^2+3x+y}{2}
$$
with uniquely determined non negative natural numbers $x,y\in \mathbb{N}_0\,.$


15. (solved by @odd_even ) Calculate
$$
S = \int_{\frac{1}{2}}^{3} \dfrac{1}{\sqrt{x^2+1}}\,\dfrac{\log(x)}{\sqrt{x}}\,dx \, + \, \int_{\frac{1}{3}}^{2} \dfrac{1}{\sqrt{x^2+1}}\,\dfrac{\log(x)}{\sqrt{x}}\,dx
$$

 

[etotheipi]

Spoiler: Question 13

I think the question was asking for a proof that F is the midpoint:

If we label up the angles in corresponding segments w, x, y and z as shown in orange below

We can see that triangles BEM and MEC are similar to AMD (by AAA). We label the angles AMF and FMD x and z respectively by the property of vertically opposite angles being equal.

Then we have two isosceles triangles, FAM and FMD, which share a common side FM. The lengths AF, FM and FD are equal. Since AF = FD, F is the midpoint of AD.

 

[fresh_42]

I think the question was asking for a proof that F is the midpoint:

If we label up the angles in corresponding segments w, x, y and z as shown in orange below

View attachment 249011

We can see that triangles BEM and MEC are similar to AMD (by AAA).

You mean BMC and AMD are similar (by the first theorem of chords in an inscribed quadrilateral)?

We label the angles AMF and FMD x and z respectively by the property of vertically opposite angles being equal.

Then we have two isosceles triangles, FAM and FMD, which share a common side FM. The lengths AF, FM and FD are equal. Since AF = FD, F is the midpoint of AD.

Yes, that was the idea. It would have been a bit more work to do if done step by step (I think). It is Brahmagupta's Theorem, named after the Indian mathematician and astronomer (598–668).

 

[Not anonymous]

(7. Show that there are infinitely many primes of the form $4k+3\, , \,k\in \mathbb{N}_0$.)

Spoiler: Question 7

Proof by contradiction. Suppose there are only a finite number of primes of the form $4k+3\, , \,k\in \mathbb{N}_0$. Let these $m$ primes be denoted by $q_1$, $q_2$, .., $q_m$, in increasing order of their value. Therefore, all other primes except 2 (the only even prime) must be of the form $4k+1\, , \,k\in \mathbb{N}_0$ (since 4k+0 and 4k+2 are even numbers and so cannot be odd primes).

Now consider the values $x = 4(\prod_{i=2}^m q_i) + 3$ and ##$(note that the product of$q_i$s starts with$q_2$, so excludes$q_1 = 3$). We observe the following: 1. Since$4(\prod_{i=2}^m q_i)$is not a multiple of 3,$4(\prod_{i=2}^m q_i) + 3$too cannot be a multiple of 3. 2. Since$4(\prod_{i=2}^m q_i)$is even,$4(\prod_{i=2}^m q_i) + 3$, i.e.$x$must be odd. 3.$x$cannot be a multiple of the other$q_i$primes (i.e.$q_2, q_3, .., q_m$) too because$4(\prod_{i=2}^m q_i)$would be a multiple of any such$q_i$and next smallest multiple divisible by$q_i$would be$4(\prod_{i=2}^m q_i) + q_i$which is greater than$x = 4(\prod_{i=2}^m q_i) + 3$(since$q_m \gt q_{m-1} \gt q_{m-2} \gt .. \gt q_2 \gt 3$). 4. Since$x$is of the form$4k+3$and by its definition must be greater than$q_m$which was assumed to be the largest prime of the form$4k+3$,$x$cannot be prime 4. Therefore,$2, q_1 = 3, q_2, .., q_m$have all been excluded as possible prime factors of$x$. By initial assumption, all other primes must be of the form$4k + 1$. So all prime factors of$x$must be of the form$4k + 1, k \in \mathbb{N}_0$, i.e. for any prime factor$p_j$of$x$, it must be that$p_j \equiv 1 \ (\mod 4)$. But it is easy to show using modular arithmetic that the product of any number of such$p_j$factors (including possible repeated values) will also be of the form$4k + 1, k \in \mathbb{N}_0$. Putting together the above observations, it follows that$x$cannot have any prime factor less than itself, implying that$x$itself is prime. Since$x \gt q_m$, this contradicts that the initial assumption that$q_m$is the largest prime of the form$4k+3, k \in \mathbb{N}_0$which in turn was a result of assuming that there are only a finite number of primes of the form$4k+3, k \in \mathbb{N}_0$. Therefore by contradiction, it follows that the number of primes of the form$4k+3, k \in \mathbb{N}_0## cannot be finite; so there must be infinite primes of that form.

 

[fresh_42]

Yes, well done! The trick with $3$ was nice. My solution didn't make that difference but was therefore a bit more complicated.

(7. Show that there are infinitely many primes of the form $4k+3\, , \,k\in \mathbb{N}_0$.)

Proof by contradiction. Suppose there are only a finite number of primes of the form $4k+3\, , \,k\in \mathbb{N}_0$. Let these $m$ primes be denoted by $q_1$, $q_2$, .., $q_m$, in increasing order of their value. Therefore, all other primes except 2 (the only even prime) must be of the form $4k+1\, , \,k\in \mathbb{N}_0$ (since 4k+0 and 4k+2 are even numbers and so cannot be odd primes).

Now consider the values $x = 4(\prod_{i=2}^m q_i) + 3$ and ##$(note that the product of$q_i$s starts with$q_2$, so excludes$q_1 = 3$). We observe the following: 1. Since$4(\prod_{i=2}^m q_i)$is not a multiple of 3,$4(\prod_{i=2}^m q_i) + 3$too cannot be a multiple of 3. 2. Since$4(\prod_{i=2}^m q_i)$is even,$4(\prod_{i=2}^m q_i) + 3$, i.e.$x$must be odd. 3.$x$cannot be a multiple of the other$q_i$primes (i.e.$q_2, q_3, .., q_m##) too ...

Or simply: $q_i\,|\,x \Longrightarrow q_i\,|\,3$ which is impossible as you excluded $3$.

... because $4(\prod_{i=2}^m q_i)$ would be a multiple of any such $q_i$ and next smallest multiple divisible by $q_i$ would be $4(\prod_{i=2}^m q_i) + q_i$ which is greater than $x = 4(\prod_{i=2}^m q_i) + 3$ (since $q_m \gt q_{m-1} \gt q_{m-2} \gt .. \gt q_2 \gt 3$).
4. Since $x$ is of the form $4k+3$ and by its definition must be greater than $q_m$ which was assumed to be the largest prime of the form $4k+3$, $x$ cannot be prime
4. Therefore, $2, q_1 = 3, q_2, .., q_m$ have all been excluded as possible prime factors of $x$. By initial assumption, all other primes must be of the form $4k + 1$. So all prime factors of $x$ must be of the form $4k + 1, k \in \mathbb{N}_0$, i.e. for any prime factor $p_j$of $x$, it must be that $p_j \equiv 1 \ (\mod 4)$. But it is easy to show using modular arithmetic that the product of any number of such $p_j$ factors (including possible repeated values) will also be of the form $4k + 1, k \in \mathbb{N}_0$.

Maybe it's a personal attitude and I should excuse myself, but I really don't like these platitudes like "easy to show". In 9 of 10 cases they cover a pit. The shortest way to you conclude is:
$$
x \equiv \prod (4k_i+1) \equiv \prod 1 \equiv 1 \equiv 4 \prod q_i +3 \equiv 3 \mod 4 \; ; \;\text{a contradiction }
$$
because modulo is a ring homomorphism. Alternatively you could name the two rules which holds:
$$
\rho(a\cdot b) \equiv \rho(a)\cdot \rho(b) \mod n \text{ and } \rho(a+ b) \equiv \rho(a)+ \rho(b) \mod n
$$
where $\rho$ is "take the remainder of the division by $n$.

Putting together the above observations, it follows that $x$ cannot have any prime factor less than itself, implying that $x$ itself is prime. Since $x \gt q_m$, this contradicts that the initial assumption that $q_m$ is the largest prime of the form $4k+3, k \in \mathbb{N}_0$ which in turn was a result of assuming that there are only a finite number of primes of the form $4k+3, k \in \mathbb{N}_0$. Therefore by contradiction, it follows that the number of primes of the form $4k+3, k \in \mathbb{N}_0$ cannot be finite; so there must be infinite primes of that form.

 

[Not anonymous]

(12. How many solutions in non-negative integers are there to the equation:

$x_1+x_2+x_3+x_4+x_5+x_6=32$​

)

Spoiler: Question 12

I assume that the order of values matters, i.e. for example, $(x_1=x_2=x_3=x_4=x_5=0, x_6 = 32)$ and $(x_1=32, x_2=x_3=x_4=x_5=x_6 = 0)$ are to be counted as 2 different solutions.

The number of possible solutions for that equation can be found using combinatorics. Each possible solution to that equation is logically equivalent to a partitioning of 32 objects into 6 bins, with some bins also allowed to be empty. Therefore, I consider the example of 32 marbles placed in a row and try to find the number of different ways in which 5 sticks can be placed between the balls or at the start or end of the row so that they partition the row of marbles into 6 groups, with some groups possibly being empty (which is equivalent to some $x_i = 0$). With 32 marbles and 5 sticks, we have 37 positions and we need to select 5 positions for placing the sticks. The number of such choices is given by ${_{37}C_5} = 435897$. Therefore, the number of possible whole-numbers-only solution for the equation $x_1+x_2+x_3+x_4+x_5+x_6=32$ is 435897.

 

[DEvens]

Spoiler: Question 9

a) By Euler's formula, the curve is $\cos^2 t \pi + i \sin t \pi \cos t \pi$ and so by the half-angle formula, the period for each of these is t from 0 to 1.

b) Let me use shorthand of $C$ for $\cos(t \pi)$ and similarly $S$ for $\sin(t \pi )$. The real part, x, is $C^2$ and the imaginary, y, is $C S$. So $x^2+y^2-x = C^4+C^2 S^2 - C^2 = C^2 (C^2+S^2-1) = 0$. Looking at the construction in part d) shows that each point on the circle so defined can be associated with a single value of t in the range 0 to 1. And so the entire circle is included.

c) From b), the function is even in y.

d) Examine the figure attached. Add the shorthand $C2$ for $\cos (2 t \pi)$, and similar for $S2$. The center of the circle in b) is the point (0.5,0), the radius is 0.5. Beginning from t=0, the point (1,0), find the arc length to a point specified by t. The x and y values are given in b). We again need the half-angle formulas. From the center of the circle to this point the y interval is just the y value of the point, or $C S = S2 / 2$. The x interval is $C^2 - 1/2 = C2/2$. So the tangent of the angle required is $S2 / C2$. That is, the angle required is $\theta = 2 t \pi$. But the radius of this circle is 0.5, so the arc length is $t \pi$. The curve is originally parameterized in its arc length divided by $\pi$, or $\gamma(t) = \gamma(\frac{s}{\pi})$.

 

[fresh_42]

a) By Euler's formula, the curve is $\cos^2 t \pi + i \sin t \pi \cos t \pi$ and so by the half-angle formula, the period for each of these is t from 0 to 1.

b) Let me use shorthand of $C$ for $\cos(t \pi)$ and similarly $S$ for $\sin(t \pi )$. The real part, x, is $C^2$ and the imaginary, y, is $C S$. So $x^2+y^2-x = C^4+C^2 S^2 - C^2 = C^2 (C^2+S^2-1) = 0$.

This shows $\gamma(\mathbb{R}) \subseteq \{\,(x,y)\in \mathbb{R}^2\,|\,x^2+y^2-x=0\,\}$, but why do those points lie on the curve?

c) From b), the function is even in y.

d) Add the shorthand $C2$ for $\cos (2 t \pi)$, and similar for $S2$. The center of the circle in b) is the point (0.5,0), the radius is 0.5. Beginning from t=0, the point (1,0), find the arc length to a point specified by t. The x and y values are given in b). We again need the half-angle formulas. From the center of the circle to this point the y interval is just the y value of the point, or $C S = S2 / 2$. The x interval is $C^2 - 1/2 = C2/2$. So the tangent of the angle required is $S2 / C2$. That is, the angle required is $2 t \pi$. But the radius of this circle is 0.5, so the arc length is $t \pi$. The curve is originally parameterized in its arc length.

I don't fully understand your proof, but the conclusion is more or less correct, depending which version of your answer we concentrate on. Could you write the formula in dependence of the arc length, say $s$?

 

[mathwonk]

For question 1,a, since for every point c, the ideal Mc of functions vanishing on c is the kernel of the evaluation map to R, a field, hence Mc is a maximal ideal, one wants to show conversely that every maximal ideal J is contained in, hence equal to, an ideal of form Mc, i.e. that J has a common zero point c. Contrapositively one wants to show that an ideal J with no common zero, is not a proper ideal, i.e. contains a unit. So assume that for every point, there is a function in the given ideal J that does not vanish at that point. Then try to use the definition of continuity, and compactness to conclude.

 

[Delta2]

I have a sketch of the proof for 2 but I need a hint on how to fully implement it.

Spoiler

We take the Riemann sum $S_n$ of the integral $$\int_0^{\pi/2}\frac{d\phi}{\sqrt{a^2\cos^2\phi+b^2\sin^2\phi}}=\lim_{n\to\infty}S_n$$ and prove by induction on $n$ that $$\frac{1}{a_n}\leq \frac{2}{\pi}S_n\leq\frac{1}{b_n}$$ and then the result follows by taking the limits and using the sandwich theorem for limits.

But I have problem with the induction... Any hints and of course am I on the right track or there is a completely different approach??

 

[fresh_42]

I have a sketch of the proof for 2 but I need a hint on how to fully implement it.

Spoiler

We take the Riemann sum $S_n$ of the integral $$\int_0^{\pi/2}\frac{d\phi}{\sqrt{a^2\cos^2\phi+b^2\sin^2\phi}}=\lim_{n\to\infty}S_n$$ and prove by induction on $n$ that $$\frac{1}{a_n}\leq \frac{2}{\pi}S_n\leq\frac{1}{b_n}$$ and then the result follows by taking the limits and using the sandwich theorem for limits.

But I have problem with the induction... Any hints and of course am I on the right track or there is a completely different approach??

This would only show, that the limits exist. It follows from $b_1 \leq b_2 \leq \ldots b_n \leq \ldots \leq a_n \leq \ldots \leq a_2 \leq a_1$.

The proof is a bit tricky. It uses a recursion $T(a,b)=T(f(a,b),g(a,b))$ with suitable $f$ and $g$.

 

[timetraveller123]

q14:

Spoiler

$let f(x,y) =\frac{{(x+y)}^2+3x+y}{2} x,y \geq 0\\$then if $n = f(x,y)$ then $n+1 = f(x+1,y-1)$ and $n-1=f(x-1,y+1)$

consider what values of n can be represented by x=0

$f(0,y) = n$ using quadratic formula we can get that n must be of the form
$n = k(2k+1)$
for positive integer k with the corresponding y being
$y = 2k$
we can then raise x by 1 and decrease y by one each time to get subsequent value of n and since y must be at least zero we have covered
$k(2k+1) \leq n \leq k(2k+1) + 2k = k (2k+3)$

similarly
$f(x,0) = n$ implies
$n = \frac{(m-1)(m+2)}{2}$
with corresponding x being
$x = m-1$
if m is odd then writing m as 2k+1 we get
$n = k(2k+3)$
this is the case previously derived
if m is even then we get
$n= (2k-1)(k+1)$
we also have that
$(2k-1)(k+1) + 1= k(2k+1)$

this is value is covered by the x=0 case
then for the case m is even we can decrease x by 1 and increase y by 1 to cover lower values of n and since x =m-1 = 2k-1 we can cover until

$(2k-1)(k+1) - (2k-1) = 2k^2-k$
we note that
$2k^2-k -1 = (k-1)(2k+1) = (k')(2k'+3)$

which has been covered before
thus all the values in between
$k(2k+1)$
and
$(k+1)(2(k+1) +1)$
is covered then i think we are done

 

[fresh_42]

Maybe it will seem a bit nitpicking, but I'll comment it as I would comment an exercise given to me for correction.

q14:

$let f(x,y) =\frac{{(x+y)}^2+3x+y}{2} x,y \geq 0\\$

Let $f(x,y) =\frac{{(x+y)}^2+3x+y}{2} \quad ; \quad x,y \geq 0$

then if $n = f(x,y)$ then $n+1 = f(x+1,y-1)$ and $n-1=f(x-1,y+1)$

The reader automatically associates a natural number with $n$. But why is $f(x,y)\in \mathbb{N}_0\,\text{?}$ You could first tell us why, but you do not need it if you write $f(x+1,y-1)=f(x,y)+1\, , \,f(x-1,y+1)=f(x,y)-1$ or the lazy way: $f(x \pm 1, y \mp 1)=f(x,y) \pm 1\;\;(*)$

consider what values of n can be represented by x=0

$f(0,y) = n$ using quadratic formula we can get that n must be of the form
$n = k(2k+1)$
for positive integer k with the corresponding y being
$y = 2k$

Same as before. What is $n$? It always looks as if you used at the beginning what you want to prove at the end. Do you assume a given $n$? Is it short for $f(0,y)$? Does your proof go: $n=f(x,y) \Longrightarrow \ldots \Longrightarrow n=\dfrac{x^2+2xy+y^2+3x+y}{2}$ Yipeeh, I wrote $n$ as required?
Short: Do not use unqualified variables!

What you considerer was: $f(0,y)=\dfrac{y^2+y}{2}=\dfrac{y(y+1)}{2}$. Now either $y$ or $y+1$ is even, so $f(0,y)\in \mathbb{N}_0$. Without loss of generality we set $y=2k$...

we can then raise x by 1 and decrease y by one each time to get subsequent value of n and since y must be at least zero we have covered
$k(2k+1) \leq n \leq k(2k+1) + 2k = k (2k+3)$

... and $k(2k+1)=f(0,y)$. With $(*)$ we get all predecessors and successors of $k(2k+1)$, hence all integers.

The existence part of the problem is finished here. You have written all natural numbers in the required way. I don't understand why you need the rest of your considerations, especially as you did not really said which role $k,n,m$ have.

similarly
$f(x,0) = n$ implies
$n = \frac{(m-1)(m+2)}{2}$
with corresponding x being
$x = m-1$
if m is odd then writing m as 2k+1 we get
$n = k(2k+3)$
this is the case previously derived
if m is even then we get
$n= (2k-1)(k+1)$
we also have that
$(2k-1)(k+1) + 1= k(2k+1)$

this is value is covered by the x=0 case
then for the case m is even we can decrease x by 1 and increase y by 1 to cover lower values of n and since x =m-1 = 2k-1 we can cover until

$(2k-1)(k+1) - (2k-1) = 2k^2-k$
we note that
$2k^2-k -1 = (k-1)(2k+1) = (k')(2k'+3)$

which has been covered before
thus all the values in between
$k(2k+1)$
and
$(k+1)(2(k+1) +1)$
is covered then i think we are done

I do not see, why this presentation of a given natural number $n$ as $n=f(x,y)$ is unique?
You are close and on the right track.

Hint: Instead of solving $f(x,y)=f(x',y') \Longrightarrow \ldots \Longrightarrow x=x'\, , \,y=y'$ which looks awful to do, consider which numbers you can cover with $s=x+y$. Observe that $(*)$ doesn't change the value of $s$. So the question is: Which interval can we cover with one specific $s$ by your method, and can there be a point in an interval for $s$ which is also in an interval for $t\neq s$?

You already had the crucial idea with $(*)$ and I think uniqueness is hidden somewhere in your argumentation, but I was unable to extract it.

 

[DEvens]

For question 10, are there some typos? Show that (a) Is F: etc. What? Maybe show that (a) If F is etc. then Phi as specified exists?

Part b includes the word "new." If $\Phi$ is just the identity, which is a smooth transformation that satisfies the requirement, then it's not a new frame but the same frame.

 

[fresh_42]

For question 10, are there some typos? Show that (a) Is F: etc. What? Maybe show that (a) If F is etc. then Phi as specified exists?

Part b includes the word "new." If $\Phi$ is just the identity, which is a smooth transformation that satisfies the requirement, then it's not a new frame but the same frame.

Yes. Lost in translation. It's corrected now.

 

[member 587159]

For question 1,a, since for every point c, the ideal Mc of functions vanishing on c is the kernel of the evaluation map to R, a field, hence Mc is a maximal ideal, one wants to show conversely that every maximal ideal J is contained in, hence equal to, an ideal of form Mc, i.e. that J has a common zero point c. Contrapositively one wants to show that an ideal J with no common zero, is not a proper ideal, i.e. contains a unit. So assume that for every point, there is a function in the given ideal J that does not vanish at that point. Then try to use the definition of continuity, and compactness to conclude.

Hi Mathwonk. That's certainly the idea for the (a) part of the question! Are you willing to fill in the details so other readers can benefit from your knowledge?

 

[mathwonk]

well sure. choose for each point t a function ft that does not vanish at t. Then there is, by the definition of continuity, an open interval It on which ft does not vanish. These intervals cover the interval J and by compactness of J, a finite number It1,...,Itn already cover it. Then the sum of the squares of the functions ft1,...,ftn, is a continuous function on J that vanishes nowhere, hence is a unit, since its inverse is again continuous.

 

[timetraveller123]

I don't understand why you need the rest of your considerations, especially as you did not really said which role k,n,mk,n,mk,n,m have.

i have made a mistake in my part 1 there is a another case i forgot to consider here is new proof

Spoiler

let n be some non negative natural number thus if
f(0,y) = n is to have a solution with y being a non negative natural then
n must be of the form either k(2k+1) or (k+1)(2k+1) with the corresponding y being 2k and 2k+1 respectively
i forgot the second case this makes the whole of second part of the previous solution irrelevant
(k+1)(2k+1) - k(2k+1) - 1 = 2k thus we can cover all numbers from (k)(2k+1) to (k+1)(2k+1) by decreasing y by 1 and increasing x by 1 each time
and since
k(2k+1) < (k+1)(2k+1) < (k+1)(2(k+1) + 1)
we have covered all the numbers in the first inequality for the second inequality we can also cover all the numbers since
(k+1)(2(k+1) + 1) - (k+1)(2k+1) -1 = 2k+1 and since this is the y value for n = (k+1)(2k+1)
we can also cover the second inequality so we have covered all integers between and including
k(2k+1) to (k+1)(2(k+1) + 1) . thus that covers all non negative integers

in my first attempt i forgot to consider the second case that made things weird.

 

[fresh_42]

Let me summarize, @timetraveller123.

Say we have a number $n=k(2k+1) \geq 0$. Then $n=f(0,2k)$. With your equations $f(x\pm 1,y\mp 1)\stackrel{(*)}{=}f(x,y)\pm 1$ we get all numbers up to $f(2k,0)= k(2k+3)=n+2k$.
On the other hand, we have $f(2k,0)=2k^2+3k=n+2k$ and by $(*)$ all numbers down to $f(0,2k)=n$, which doesn't give us new numbers.

So we look at $f(0,2k-1)=2k^2-k=k(2k-1)=n-2k$ and by $(*)$ all numbers up to $f(2k-1,0)=2k^2+k-1=n-1$

Both "machines" give us therefore all numbers form $n-2k, n-2k+1,\ldots,n-1,n,n+1,n+2k$.

$k=0$ yields $n=0$.
$k=1$ yields $n=1\cdot (2\cdot 1 +1)=3$ and the "machine" outputs $3-2,3-1,\ldots,3+2=1,2,3,4,5$.
$k=2$ yields $n=2\cdot (2\cdot 2 +1)=10$ and the "machine" outputs $10-2\cdot 2=6,\ldots ,14$.

And so on is o.k., an induction exaggerated, but we can write:

After the numbers $n-2k,\ldots ,n+2k$ we increase $k$ by one and get as new values $k'=k+1$ and $n'=k'(2k'+1)=(k+1)(2(k+1)+1)= 2k^2+5k+3$. Then our "machine" yields all numbers from $n'-2k'=2k^2+5k+3-2k-2=2k^2+3k+1=k(2k+1)+2k+1=n+2k+1$ which is the next number our "machine" hasn't produced with $k$, but does so with $k+1$.

Sorry, I had to sort out your strategy for myself to understand what you have. At this point we have all numbers covered, AND the intervals produced by the "machine" for one specific value $k$ do not intersect with those of other values, i.e. uniqueness for $x,y$ in $n=f(x,y)$ is also given.

 

[timetraveller123]

yes that is what i meant

 

[StoneTemplePython]

No one ever does the matrix problems...
This one is quite nice and relates to a favorite topic of mine: Gram matrices, as well as rudimentary geometry.
There may be a more expedient route but I used a rank based argument. This ended up being a bit longer than I had hoped...

Problem 3
$\mathbf W = \begin{bmatrix} 0&1&1&1&1 \\ 1&0&|AB|^2&|AC|^2&|AD|^2 \\ 1&|AB|^2&0&|BC|^2&|BD|^2 \\ 1&|AC|^2&|BC|^2&0&|CD|^2 \\ 1&|AD|^2&|BD|^2&|CD|^2&0 \end{bmatrix} = \begin{bmatrix} 0 &\mathbf 1^T \\\mathbf 1 & \mathbf W_p\end{bmatrix}$

where $\mathbf W_p$ is the principal submatrix of main interest
we need to prove $\operatorname{det}\big(\mathbf W\big) = 0$

lemma
The sum of $d$ rank one updates has rank at most $d$.

This is implied by familiar matrix multiplication rank properties.
$\mathbf S \in \mathbb R^{\text{d x n}}$ and conforming $\mathbf C$, so

$\mathbf C\mathbf S$
$= \bigg[\begin{array}{c|c|c|c|c} \mathbf c_1 & \mathbf c_2 &\cdots & \mathbf c_{d-1} & \mathbf c_{d} \end{array}\bigg]\begin{bmatrix} \tilde{ \mathbf s_1}^T \\ \tilde{ \mathbf s_2}^T \\ \vdots\\ \tilde{ \mathbf s}_{d-1}^T \\ \tilde{ \mathbf s}_d^T \end{bmatrix}$
$= \mathbf c_1 \tilde{ \mathbf s_1}^T + \mathbf c_2 \tilde{ \mathbf s_2}^T +... + \mathbf c_d \tilde{ \mathbf s_d}^T$
$= \sum_{k=1}^d\mathbf c_k \tilde{ \mathbf s_k}^T$

so
$\text{rank}\Big(\sum_{k=1}^d\mathbf c_k \tilde{ \mathbf s_k}^T\Big)= \text{rank}\Big(\mathbf C\mathbf S\Big) \leq \text{rank}\Big(\mathbf S\Big) \leq \min\Big(d,n\Big) \leq d$

Spoiler

Geometrically pleasant special case:
suppose all of these points (A,B,C,D --> relabelled as 1,2,3,4 or $\mathbf x_1, \mathbf x_2, \mathbf x_3, \mathbf x_4$ ) are in the plane, and this mysterious column zero is also in the plane. In effect we can interpret point 0 as the origin.

It isn't needed, but the geometry associated with this very nice in this special case: the above squared distance matrix, suggests that in effect point zero is the origin and points 1,2,3,4 are all (squared) distance of 1 from it -- i.e. they are on the boundary of the unit circle.

In general, the idea is that we have $m$ points and we know the (squared) distance between them. And we know the distance was created by use of an inner product (and specifically via standard dot product of vectors $\in \mathbb R^2$). In general whenever have have an inner product, I've suggested that its wise to try to look at the Gram Matrix $\mathbf G$. So we have

$2\mathbf G = -\mathbf W + \mathbf 1\mathbf y^T + \mathbf y \mathbf 1^T$
where $\mathbf y$ is a vector containing the original squared 2-norm of points $\mathbf x_k$ --we have 5 in this case, but it is useful to think in general of $m$ points and $\mathbf G \in \mathbb R^\text{m x m}$

examine component i,j of this matrix to verify that
$2\cdot g_{i,j}$
$= -\big \Vert \mathbf x_i - \mathbf x_j\big \Vert_2^2 + \big\Vert \mathbf x_i\big\Vert_2^2 + \big\Vert \mathbf x_j \big\Vert_2^2$
$= -\Big\{\langle \mathbf x_i - \mathbf x_j, \mathbf x_i - \mathbf x_j\rangle \Big\}+ \langle \mathbf x_i, \mathbf x_i\rangle+ \langle \mathbf x_j, \mathbf x_j\rangle$
$=-\Big\{ \langle \mathbf x_i, \mathbf x_i\rangle + \langle \mathbf x_j, \mathbf x_j\rangle - 2\langle \mathbf x_i , \mathbf x_j\rangle \Big\}+ \langle \mathbf x_i, \mathbf x_i\rangle+ \langle \mathbf x_j, \mathbf x_j\rangle$
$= 2\langle \mathbf x_i , \mathbf x_j\rangle$

which confirms that $\mathbf G$ is a Gram Matrix. Since we know these points are in $\mathbb R^2$, we know that in fact

$\mathbf X^T\mathbf X = \mathbf G$
$\mathbf X = \bigg[\begin{array}{c|c|c|c} \mathbf x_0 &\mathbf x_1 &\cdots & \mathbf x_{m-1} \end{array}\bigg]$
where $\mathbf X \in \mathbb R^{\text{2 x m}}$

hence
$\text{rank}\big(\mathbf G \big) = \text{rank}\big(\mathbf X^T\mathbf X \big) =\text{rank}\big(\mathbf X\big) \leq d = 2$
and in particular we can use the 'outer product/rank one update' interpretation of matrix multiplication to write $\mathbf X^T \mathbf X$ as a the sum of (at most) 2 rank one matrices. For avoidance of doubt revisit the lemma and let $\mathbf C:= \mathbf X^T$ and $\mathbf S := \mathbf X$ and of course $d =2$ and $n=m$.

so
$\mathbf G = \sum_{k=1}^2\mathbf c_k \tilde{ \mathbf s_k}^T$

the fact that this holds up to rescaling suggests it would be nicer to write
$-2\mathbf G := \sum_{k=1}^2\mathbf c_k \tilde{ \mathbf s_k}^T$
So I use this going forward -- if its an issue I can introdue more notation I suppose

But we know
$\mathbf W= -2\mathbf G + \mathbf 1\mathbf y^T + \mathbf y \mathbf 1^T = \big(\sum_{k=1}^2\mathbf c_k \tilde{ \mathbf s_k}^T\big) +\mathbf 1\mathbf y^T + \mathbf y \mathbf 1^T = \big(\sum_{k=1}^4\mathbf c_k \tilde{ \mathbf s_k}^T\big)$
(after re-labelling)

which allows us to conclude
$\text{rank}\big(\mathbf W\big) \leq 4 \lt 5 \longrightarrow \det\big(\mathbf W\big) = 0$

algebraic tweak for the more general case
The above was nice but technically we don't know anything about $\mathbf x_0$, whether it actually exists in the plane, etc. The hack is to just zero out the thing we are unsure of re-run the above argument with just

$\mathbf X = \bigg[\begin{array}{c|c|c|c|c} \mathbf 0 &\mathbf x_1 &\cdots & \mathbf x_{m-1} \end{array}\bigg]$

i.e. to get
$\mathbf G = \begin{bmatrix} 0 &\mathbf 0^T \\\mathbf 0 & \mathbf G_p\end{bmatrix}$
where $\mathbf G_p$ is a principal submatrix of interest.
Equivalently we are re-running the above argument with $m=4$ not $m=5$ this time, and then zero padding the result.

and we consider
$\mathbf y := \begin{bmatrix} 0 \\ \mathbf y_p\end{bmatrix}$

where $\mathbf y_p$ is the 'real result' associated with those 4 points, i.e. associated with the principal submatrix. Putting this together gives

$\mathbf W_{\text{almost}}= -2\mathbf G + \mathbf 1\mathbf y^T + \mathbf y \mathbf 1^T = \begin{bmatrix} 0 &\mathbf 0^T \\\mathbf 0 & \mathbf W_p\end{bmatrix}$

our above argument says that
$\text{rank}\Big(\mathbf W_{\text{almost}}\Big)$
$= \text{rank}\Big(\big(\sum_{k=1}^2\mathbf c_k \tilde{ \mathbf s_k}^T\big)+ \mathbf 1\mathbf y^T + \mathbf y \mathbf 1^T\Big)$
$= \text{rank}\Big(\sum_{k=1}^4\mathbf c_k \tilde{ \mathbf s_k}^T\Big)$
$\leq 4$
$\lt 5$

so
$\det\Big(\mathbf W_{\text{almost}}\Big)=0$

This appears to be a weak result since we can eyeball the column of all zeros and see that $\mathbf W_{\text{almost}}$ is singular. But if we notice the homogeneity in the components of the first row and column (all ones except for the diagonal) we can hack our way to the desired result:

$\mathbf D := \begin{bmatrix} -1 &\mathbf 0^T \\\mathbf 0 & \mathbf I_p\end{bmatrix}$
$\mathbf y_1 := \begin{bmatrix} 1 \\ \mathbf y_p\end{bmatrix}$
$\mathbf y_2 := \begin{bmatrix} -1 \\ \mathbf y_p\end{bmatrix}$
i.e. $\mathbf y_2 = \mathbf D\mathbf y_1$
- - - -
so
$-2\mathbf G + \mathbf 1\mathbf y_1^T + \mathbf y_2 \mathbf 1^T = \begin{bmatrix} 0 &-\mathbf 1^T \\\mathbf 1 & \mathbf W_p\end{bmatrix}$
i.e.
$\mathbf D\mathbf W = -2\mathbf G + \mathbf 1\mathbf y_1^T + \mathbf y_2 \mathbf 1^T$

making use of the involution, $\mathbf D^2 = \mathbf I$, and the fact that multiplication by invertible matrices doesn't change the rank, we have
$\text{rank}\Big(\mathbf W\Big) = \text{rank}\Big(\mathbf D^2\mathbf W\Big) = \text{rank}\Big(\mathbf D\mathbf W\Big) \leq 4 \lt 5 \longrightarrow \det\Big(\mathbf W\Big) =0$

which completes the proof.

 

[fresh_42]

No one ever does the matrix problems...
This one is quite nice and relates to a favorite topic of mine: Gram matrices, as well as rudimentary geometry.
There may be a more expedient route but I used a rank based argument. This ended up being a bit longer than I had hoped...

Problem 3
$\mathbf W = \begin{bmatrix} 0&1&1&1&1 \\ 1&0&|AB|^2&|AC|^2&|AD|^2 \\ 1&|AB|^2&0&|BC|^2&|BD|^2 \\ 1&|AC|^2&|BC|^2&0&|CD|^2 \\ 1&|AD|^2&|BD|^2&|CD|^2&0 \end{bmatrix} = \begin{bmatrix} 0 &\mathbf 1^T \\\mathbf 1 & \mathbf W_p\end{bmatrix}$

where $\mathbf W_p$ is the principal submatrix of main interest
we need to prove $\operatorname{det}\big(\mathbf W\big) = 0$

lemma
The sum of $d$ rank one updates has rank at most $d$.

This is implied by familiar matrix multiplication rank properties.
$\mathbf S \in \mathbb R^{\text{d x n}}$ and conforming $\mathbf C$, so

$\mathbf C\mathbf S$
$= \bigg[\begin{array}{c|c|c|c|c} \mathbf c_1 & \mathbf c_2 &\cdots & \mathbf c_{d-1} & \mathbf c_{d} \end{array}\bigg]\begin{bmatrix} \tilde{ \mathbf s_1}^T \\ \tilde{ \mathbf s_2}^T \\ \vdots\\ \tilde{ \mathbf s}_{d-1}^T \\ \tilde{ \mathbf s}_d^T \end{bmatrix}$
$= \mathbf c_1 \tilde{ \mathbf s_1}^T + \mathbf c_2 \tilde{ \mathbf s_2}^T +... + \mathbf c_d \tilde{ \mathbf s_d}^T$
$= \sum_{k=1}^d\mathbf c_k \tilde{ \mathbf s_k}^T$

so
$\text{rank}\Big(\sum_{k=1}^d\mathbf c_k \tilde{ \mathbf s_k}^T\Big)= \text{rank}\Big(\mathbf C\mathbf S\Big) \leq \text{rank}\Big(\mathbf S\Big) \leq \min\Big(d,n\Big) \leq d$

Spoiler

Geometrically pleasant special case:
suppose all of these points (A,B,C,D --> relabelled as 1,2,3,4 or $\mathbf x_1, \mathbf x_2, \mathbf x_3, \mathbf x_4$ ) are in the plane, and this mysterious column zero is also in the plane. In effect we can interpret point 0 as the origin.

It isn't needed, but the geometry associated with this very nice in this special case: the above squared distance matrix, suggests that in effect point zero is the origin and points 1,2,3,4 are all (squared) distance of 1 from it -- i.e. they are on the boundary of the unit circle.

In general, the idea is that we have $m$ points and we know the (squared) distance between them. And we know the distance was created by use of an inner product (and specifically via standard dot product of vectors $\in \mathbb R^2$). In general whenever have have an inner product, I've suggested that its wise to try to look at the Gram Matrix $\mathbf G$. So we have

$2\mathbf G = -\mathbf W + \mathbf 1\mathbf y^T + \mathbf y \mathbf 1^T$
where $\mathbf y$ is a vector containing the original squared 2-norm of points $\mathbf x_k$ --we have 5 in this case, but it is useful to think in general of $m$ points and $\mathbf G \in \mathbb R^\text{m x m}$

examine component i,j of this matrix to verify that
$2\cdot g_{i,j}$
$= -\big \Vert \mathbf x_i - \mathbf x_j\big \Vert_2^2 + \big\Vert \mathbf x_i\big\Vert_2^2 + \big\Vert \mathbf x_j \big\Vert_2^2$
$= -\Big\{\langle \mathbf x_i - \mathbf x_j, \mathbf x_i - \mathbf x_j\rangle \Big\}+ \langle \mathbf x_i, \mathbf x_i\rangle+ \langle \mathbf x_j, \mathbf x_j\rangle$
$=-\Big\{ \langle \mathbf x_i, \mathbf x_i\rangle + \langle \mathbf x_j, \mathbf x_j\rangle - 2\langle \mathbf x_i , \mathbf x_j\rangle \Big\}+ \langle \mathbf x_i, \mathbf x_i\rangle+ \langle \mathbf x_j, \mathbf x_j\rangle$
$= 2\langle \mathbf x_i , \mathbf x_j\rangle$

which confirms that $\mathbf G$ is a Gram Matrix. Since we know these points are in $\mathbb R^2$, we know that in fact

$\mathbf X^T\mathbf X = \mathbf G$
$\mathbf X = \bigg[\begin{array}{c|c|c|c} \mathbf x_0 &\mathbf x_1 &\cdots & \mathbf x_{m-1} \end{array}\bigg]$
where $\mathbf X \in \mathbb R^{\text{2 x m}}$

hence
$\text{rank}\big(\mathbf G \big) = \text{rank}\big(\mathbf X^T\mathbf X \big) =\text{rank}\big(\mathbf X\big) \leq d = 2$
and in particular we can use the 'outer product/rank one update' interpretation of matrix multiplication to write $\mathbf X^T \mathbf X$ as a the sum of (at most) 2 rank one matrices. For avoidance of doubt revisit the lemma and let $\mathbf C:= \mathbf X^T$ and $\mathbf S := \mathbf X$ and of course $d =2$ and $n=m$.

so
$\mathbf G = \sum_{k=1}^2\mathbf c_k \tilde{ \mathbf s_k}^T$

the fact that this holds up to rescaling suggests it would be nicer to write
$-2\mathbf G := \sum_{k=1}^2\mathbf c_k \tilde{ \mathbf s_k}^T$
So I use this going forward -- if its an issue I can introdue more notation I suppose

But we know
$\mathbf W= -2\mathbf G + \mathbf 1\mathbf y^T + \mathbf y \mathbf 1^T = \big(\sum_{k=1}^2\mathbf c_k \tilde{ \mathbf s_k}^T\big) +\mathbf 1\mathbf y^T + \mathbf y \mathbf 1^T = \big(\sum_{k=1}^4\mathbf c_k \tilde{ \mathbf s_k}^T\big)$
(after re-labelling)

which allows us to conclude
$\text{rank}\big(\mathbf W\big) \leq 4 \lt 5 \longrightarrow \det\big(\mathbf W\big) = 0$

algebraic tweak for the more general case
The above was nice but technically we don't know anything about $\mathbf x_0$, whether it actually exists in the plane, etc. The hack is to just zero out the thing we are unsure of re-run the above argument with just

$\mathbf X = \bigg[\begin{array}{c|c|c|c|c} \mathbf 0 &\mathbf x_1 &\cdots & \mathbf x_{m-1} \end{array}\bigg]$

i.e. to get
$\mathbf G = \begin{bmatrix} 0 &\mathbf 0^T \\\mathbf 0 & \mathbf G_p\end{bmatrix}$
where $\mathbf G_p$ is a principal submatrix of interest.
Equivalently we are re-running the above argument with $m=4$ not $m=5$ this time, and then zero padding the result.

and we consider
$\mathbf y := \begin{bmatrix} 0 \\ \mathbf y_p\end{bmatrix}$

where $\mathbf y_p$ is the 'real result' associated with those 4 points, i.e. associated with the principal submatrix. Putting this together gives

$\mathbf W_{\text{almost}}= -2\mathbf G + \mathbf 1\mathbf y^T + \mathbf y \mathbf 1^T = \begin{bmatrix} 0 &\mathbf 0^T \\\mathbf 0 & \mathbf W_p\end{bmatrix}$

our above argument says that
$\text{rank}\Big(\mathbf W_{\text{almost}}\Big)$
$= \text{rank}\Big(\big(\sum_{k=1}^2\mathbf c_k \tilde{ \mathbf s_k}^T\big)+ \mathbf 1\mathbf y^T + \mathbf y \mathbf 1^T\Big)$
$= \text{rank}\Big(\sum_{k=1}^4\mathbf c_k \tilde{ \mathbf s_k}^T\Big)$
$\leq 4$
$\lt 5$

so
$\det\Big(\mathbf W_{\text{almost}}\Big)=0$

This appears to be a weak result since we can eyeball the column of all zeros and see that $\mathbf W_{\text{almost}}$ is singular. But if we notice the homogeneity in the components of the first row and column (all ones except for the diagonal) we can hack our way to the desired result:

$\mathbf D := \begin{bmatrix} -1 &\mathbf 0^T \\\mathbf 0 & \mathbf I_p\end{bmatrix}$
$\mathbf y_1 := \begin{bmatrix} 1 \\ \mathbf y_p\end{bmatrix}$
$\mathbf y_2 := \begin{bmatrix} -1 \\ \mathbf y_p\end{bmatrix}$
i.e. $\mathbf y_2 = \mathbf D\mathbf y_1$
- - - -
so
$-2\mathbf G + \mathbf 1\mathbf y_1^T + \mathbf y_2 \mathbf 1^T = \begin{bmatrix} 0 &-\mathbf 1^T \\\mathbf 1 & \mathbf W_p\end{bmatrix}$
i.e.
$\mathbf D\mathbf W = -2\mathbf G + \mathbf 1\mathbf y_1^T + \mathbf y_2 \mathbf 1^T$

making use of the involution, $\mathbf D^2 = \mathbf I$, and the fact that multiplication by invertible matrices doesn't change the rank, we have
$\text{rank}\Big(\mathbf W\Big) = \text{rank}\Big(\mathbf D^2\mathbf W\Big) = \text{rank}\Big(\mathbf D\mathbf W\Big) \leq 4 \lt 5 \longrightarrow \det\Big(\mathbf W\Big) =0$

which completes the proof.

I have found this problem in Tery's Newsletter to his Blog. It is the Cayley Menger Determinant. Your algebraic and his proof are along the same idea: Use $|AB|^2=|A|^2\cdot|B|^2 -2A\cdot B$ and write the matrix $W=M+M^\tau-2G$ where $M$ has the rows $1,|A|^2,|B|^2,|C|^2,|D|^2$ and is thus of rank $1$ and $G$ are all the inner products, surrounded by zeroes in the first column and row.

The coclusion then goes:
$\operatorname{rk}M = \operatorname{rk}M^\tau = 1$ and $G=S\cdot S^\tau$ with the $5 \times 2$ matrix with rows $0,A,B,C,D$, i.e. $\operatorname{rk}G \leq 2$. Hence $\operatorname{rk}\left( M+M^\tau -2G\right) \leq 1+1+2=4<5$ and its determinant vanishes.

 

[DEvens]

Oh man! I hit the cancel button after typing in my whole answer. Try again.

Spoiler: Question 10

For the following I will be using that SO(n) is a group and that $\{ e_i \}$ is a basis for it. So if $F e_1 = T$ then $F^{-1} T = e_1$.

a) Given $F e_1 = F_0 e_1 = T$ then by group properties the inverse of $F$ and $F_0$ must exist.

Try $\Phi = F_0^{-1} F$.

Then $F_0 \Phi = F_0 F_0^{-1} F = F$, so the first part is true. And $\Phi e_1 = F_0^{-1} F e_1 = F_0^{-1} T = F_0^{-1} F_0 e_1 = e_1$ so the second part is true.

b) Since $\Phi e_1 = e_1$ and $F_0 e_1 = T$ then $F e_1 = F_0 \Phi e_1 = F_0 e_1 = T$. That is, $F$ gives a frame also. Whether it is distinct depends on $\Phi$.

c) Start with $F= F_0 \Phi$ and take the time derivative.

$\frac{d F}{dt} = F A = \frac{d F_0} {dt} \Phi + F_0 \Phi^{\prime} = F_0 A_0 \Phi + F_0 \Phi^{\prime}$

Now use that $(AB)^{-1} = B^{-1} A^{-1}$ and multiply the whole thing by $F^{-1}$.

$A = F^{-1} F_0 A_0 \Phi +F^{-1} F_0 \Phi^{\prime}$
$= (F_0^{-1} F)^{-1} A_0 \Phi +(F_0^{-1} F)^{-1}\Phi^{\prime}$
$= \Phi^{-1} A_0 \Phi +\Phi^{-1}\Phi^{\prime}$

 

[DEvens]

I have updated my post in 7. Can you please have a look?

 

[fresh_42]

The curve is originally parameterized in its arc length divided by $\pi, or \gamma(t) = \gamma(\frac{s}{\pi}).$

Or a bit more detailed: $p(s)=\gamma(\Phi(s))=\gamma\left(\dfrac{s}{\pi}\right) = \cos(s)\cdot e^{is}$.
I had hoped for the arc length integral and a calculation why $\gamma$ solves the circle equation for our youngsters to follow the argumentation, but o.k.

 

[Not anonymous]

11. Show that the number of ways to express a positive integer $n$ as the sum of consecutive positive integers is equal to the number of odd factors of $n$.

I am forced to assume that @fresh_42 meant to say "number of odd factors other than (i.e. excluding) 1", because otherwise it is easy to find counter-examples. There is just one way to write 6 as a sum of consecutive natural numbers ($1+2+3$) even though it has two odd factors, 1 and 3.

I am giving below one way to prove the claim stated in the question, but the proof isn't rigorous. I will work out the finer details and post it later when I have some free time.

Spoiler: Question 11 (Partial solution)

Observation 1: Any odd natural number $y >= 3$ can be written as a sum of 2 consecutive positive integers, $(y -1)/2$ and $(y+1)/2$

Observation 2: If a sequence of consecutive natural numbers is an odd-length sequence "centered" at an integer $x$ (e.g. $4, 5, 6$ is centered at $x=5$ and is of length 3), then the sequence's sum is $x * lengthOfSequence$. The length of such an odd-length sequence can be denoted by $(2k + 1)$. $k$ will be the count of numbers to the left of $x$ and also the count of numbers to the right of $x$. It is easy to see that every pair of numbers that are at the same offset to the left and to the right of $x$ in the sequence will add up to $2x$ and the sum is $(2k+ 1)*x$.

Observation 3: If such an odd-length sequence is centered at an odd number and the sequence starts sufficiently away from 1 (away-ness dependent on $k$, need to work out the exact formula), then it can be transformed or broken down to an even-length sequence of consecutive natural numbers that is double the length but adds up to the same sum as the original sequence; this even-length sequence will be centered around 2 consecutive numbers derived from the original center $x$ as per observation 1. E.g. $(6 + 7 + 8) \equiv ((1+2)+(3+4)+(5+6)) \equiv 21$

Observation 4: If the consecutive numbers sequence is of even-length or if it centered at an even number, then there is no transformation to a longer sequence of consecutive numbers (like that in previous observation) that adds up to same sum.

Now suppose there are $m$ distinct ways to factorize $n$ as a multiple of 2 numbers and they are represented as $a_{1} \times b_{1}, a_{2} \times b_{2}, ..., a_{m} \times b_{m}$ where $a_{i} <= b_{i}$. Also we order then such that $a{1} < a_{2} < ... < a_{m}$. We can map each such pair to atmost two unique sequences of consecutive natural number that add up to $n$. The mapping will be as follows:

• If $a_{1} = 1$, then we can map to just one sequence, $(b{1} -1)/2 + (b{1} +1)/2$, provided $b$ is odd. No mapping if $b_{1} = n$ is even
• If $a_{i} and b_{i}$ are even, then no mapping
• If both $a_{i}$ and $b_{i}$ are odd, then we map to $(b_{i} - ((a_{i}-1) \div 2)), (b_{i} - ((a_{i}-1) \div 2) +1), .., b_{i}, (b_{i} + 1), .., (b_{i} + ((a_{i}-1) \div 2))$, i.e. an odd-length sequence centered at an odd number. This sequence can be broken down to another sequence based on obsrvation 3, so we get 2 mappings
• If only one $a_{i}$ and $b_{i}$ is odd, then only one mapping is possible

If we use the above transformations, we get as many sequences that add up to $n$ as there are odd factors of $n$ (except for the odd factor 1)

 

[fresh_42]

11. Show that the number of ways to express a positive integer $n$ as the sum of consecutive positive integers is equal to the number of odd factors of $n$.

I am forced to assume that @fresh_42 meant to say "number of odd factors other than (i.e. excluding) 1", because otherwise it is easy to find counter-examples. There is just one way to write 6 as a sum of consecutive natural numbers ($1+2+3$) even though it has two odd factors, 1 and 3.

Yes, $1$ isn't considered a factor, since you can always multiply as many units as you want and get any number of factors. Btw. $-1$ is also a unit, so you could argue that $-1,1,3,-3$ are four odd factors of $6$. It simply makes no sense to allow units.

You're thinking way too complicated. Just calculate $n=r+(r+1)+\ldots + (r+k)$ and examine the factors.

 

[StoneTemplePython]

I have found this problem in Tery's Newsletter to his Blog. It is the Cayley Menger Determinant. Your algebraic and his proof are along the same idea: Use $|AB|^2=|A|^2\cdot|B|^2 -2A\cdot B$ and write the matrix $W=M+M^\tau-2G$ where $M$ has the rows $1,|A|^2,|B|^2,|C|^2,|D|^2$ and is thus of rank $1$ and $G$ are all the inner products, surrounded by zeroes in the first column and row.

The coclusion then goes:
$\operatorname{rk}M = \operatorname{rk}M^\tau = 1$ and $G=S\cdot S^\tau$ with the $5 \times 2$ matrix with rows $0,A,B,C,D$, i.e. $\operatorname{rk}G \leq 2$. Hence $\operatorname{rk}\left( M+M^\tau -2G\right) \leq 1+1+2=4<5$ and its determinant vanishes.

Yea... I woke up today not liking my finish. It seems to me a nice way might be to use a well chosen Projector with rank 4 or (m-1) and argue by contradiction that if $\text{rank}\big(\mathbf W\big) = 5$ or (= m), then

$3$
$= (m-1) +(m-1) -m$
$= \text{rank}\Big(\big(\mathbf P\mathbf W\big)\Big) + \text{rank}\Big(\mathbf P\Big) - m$
$\leq \text{rank}\Big(\big(\mathbf P\mathbf W\big)\mathbf P\Big)$
$= \text{rank}\Big(\mathbf P\mathbf W\mathbf P\Big)$
$\leq 2$

with

$\mathbf q = \begin{bmatrix} 0 \\ \mathbf 1 \end{bmatrix} = \sum_{k=2}^m \mathbf e_k$
$\mathbf P = \mathbf I_m -\frac{1}{m-1}\mathbf {qq}^T$


I don't really prefer contradictions typically but the projection really is just sitting there... A couple more details should make this into a nice solution instead of the rather messy thing I've written.

edit:

(where for avoidance of doubt we have standard basis vectors $\mathbf e_k$)

Spoiler

$\mathbf W = \begin{bmatrix} 0 &\mathbf 1^T \\\mathbf 1 & \mathbf W_p\end{bmatrix} = \begin{bmatrix} 0 &\mathbf 0^T \\\mathbf 0 & \mathbf W_p\end{bmatrix} + \mathbf e_1 \mathbf q^T + \mathbf q\mathbf e_1^T$

Then
$\mathbf P\mathbf W \mathbf P = \mathbf P\begin{bmatrix} 0 &\mathbf 0^T \\\mathbf 0 & \mathbf W_p\end{bmatrix}\mathbf P + \mathbf P\mathbf e_1 \big(\mathbf q^T\mathbf P\big) + \big(\mathbf P \mathbf q\big)\mathbf e_1^T\mathbf P = \mathbf P\begin{bmatrix} 0 &\mathbf 0^T \\\mathbf 0 & \mathbf W_p\end{bmatrix}\mathbf P$

so we need to examine
$\mathbf P\begin{bmatrix} 0 &\mathbf 0^T \\\mathbf 0 & \mathbf W_p\end{bmatrix}\mathbf P$
$= \begin{bmatrix} 1 &\mathbf 0^T \\\mathbf 0 & \mathbf P_p\end{bmatrix}\begin{bmatrix} 0 &\mathbf 0^T \\\mathbf 0 & \mathbf W_p\end{bmatrix} \begin{bmatrix} 1 &\mathbf 0^T \\\mathbf 0 & \mathbf P_p\end{bmatrix}$
$= \begin{bmatrix} 0 &\mathbf 0^T \\\mathbf 0 & \mathbf P_p\mathbf W_p\mathbf P_p\end{bmatrix}$

but this principal submatrix $\mathbf P_p$ is also a projector in nominal (m-1) dimensional space --a nice overlapping sub-problem
$\mathbf P_p = \mathbf I - \frac{1}{m-1} \mathbf {11}^T$

then
$\mathbf P_p\mathbf W_p\mathbf P_p= \mathbf P_p\big(\big(\sum_{k=1}^2\mathbf c_k \tilde{ \mathbf s_k}^T\big) +\mathbf 1\mathbf y^T + \mathbf y \mathbf 1^T\big)\mathbf P_p =\sum_{k=1}^2\mathbf P_p\mathbf c_k \tilde{ \mathbf s_k}^T\mathbf P_p$
because this projector annhilates the ones vector

so
$\text{rank}\big(\mathbf P\mathbf W \mathbf P\big) = \text{rank}\big(\mathbf P_p\mathbf W_p\mathbf P_p\big) \leq 2$
because we have the sum of (at most) 2 rank one updates

this gives the 'upper bound' on rank. The 'lower bound' is due to basic properties of rank with multiplication and
$3 \leq \text{rank}\Big(\mathbf P\mathbf W\mathbf P\Big)\leq 2$
is an obvious contradiction, forced on us by the assumption that $\mathbf W$ was non-singular
[\SPOILER]

the approach on Tao's blog is more succinct and direct, though I find the projector here curiously satisfying

 

[fresh_42]

Oh man! I hit the cancel button after typing in my whole answer.

In such cases, duplicate the tab to create a test area, and update the page (F5). The PF software has probably saved most of your reply, i.e. up to the last two lines or so. Another idea is to use the backwards arrow of the browser, but I'm not sure about the result.

 

[fresh_42]

the approach on Tao's blog is more succinct and direct, though I find the projector here curiously satisfying

I liked the idea to write a symmetric square matrix as a product of a rectangular matrix and its transpose to find an upper bound for the rank. I think this is a useful trick in similar situations.

 

[Not anonymous]

Yes, $1$ isn't considered a factor, since you can always multiply as many units as you want and get any number of factors. Btw. $-1$ is also a unit, so you could argue that $-1,1,3,-3$ are four odd factors of $6$. It simply makes no sense to allow units.

You're thinking way too complicated. Just calculate $n=r+(r+1)+\ldots + (r+k)$ and examine the factors.

Thanks to @fresh_42 for the hint! The answer is too obvious after that. I merely add some formalism for the sake of completeness. Before my earlier attempt, I had briefly considered working backward from the formula for sum of sequence as suggested by the hint but didn't proceed along that line as I thought I could arrive at a more "intuitive" solution that didn't need formulae, and that made giving a proof more complex that needed.

(11. Show that the number of ways to express a positive integer $n$ as the sum of consecutive positive integers is equal to the number of odd factors of $n$.)

Spoiler: Question 11

Any sequence of $k$ consecutive integers can be written as $a+1, a+2, ..., a+k$. Here $a+1$ is the 1st integer in the sequence. The sum of this sequence is $ka + \frac {k(k+1)} {2} = k(a + \frac {k+1} {2})$. We consider positive integer values for $k$, i.e. $k \in \{2, 3, 4, .., \}$ (since $k$ is the length of a non-empty sequence, it must be a positive integer). We ignore $k=1$ as that will correspond to the degenerate case of single-element sequence $(n)$, whereas the question apparently considers only sequences having more than 1 integer (except when $n$ itself is 1, in which case there is exactly one sequence satisfying the criteria, $\{1\}$).

• We inspect values of $k \in \{2, 3, .., \}$ and look for the value of $a$ such that the sum of the sequence $a+1, a+2, .., a+k$ sums to $n$, i.e. $$k(a + \frac {k+1} {2}) = n$$.
• If $k$ is NOT a factor of $n$, then $(a + \frac {k+1} {2})$ would be non-integer in the above equation, implying that there is no integer $a$ such that a $k$-length integer sequence will add up to $n$, so we only need to consider those values of $k$ that are factors of $n$.
• If $k$ is even, then $\frac {k+1} {2}$ would be a non-integer, so again (even if that $k$ is a factor of $n$), there would be no $k$-length integer sequence that adds up to $n$
• If $k$ is an odd factor of $n$, then $\frac {k+1} {2}$ is an integer and we can find an integer value for $a$ such that the $k$-long sequence starting at $a+1$ adds up to $n$. $a$ is given by the equation $$a = \frac {n} {k} - \frac {k+1} {2}$$
• The value of $a$ from the above equation could be negative, whereas we want only sequences that consist of positive integers alone. It is easy to show that any integer sequence $a+1, a+2, .. a+k$ that adds up to a positive value can be reduced to a positive integer sub-sequence if the original sequence starts with zero or a negative integer
  • If the sequence starts with 0, will simply drop that as removing 0 does not alter the sum of the sequence​
  • If the sequence starts with a negative number and yet adds up to a positive number, then it must be the case that the sequence is of the form $-x, -x+1, -x+2, ..., 0, 1, .., x, x+1, .., x+j$ (for some positive integers $x, j$ satisfying the condition $x = -(a+1)$, $x+j = (a+k)$), i.e. for every negative integer $-y$, the sequence should also contain the positive integer $y$ and the number of positive integers in the sequence should exceed the number of negative integers in the sequence. In effect, the negative integers get canceled out by their positive counterparts in the summation, so we can trim a left portion of original sequence and get a positive-integers-only sequence ($(x+1, x+2, ..., x+j)$) that adds up to the same value as the original sequence.​

Thus, for every odd-factor $k$ of $n$, we can find a unique sequence of consecutive positive integers that sum to $n$ whereas no such sequence would exist for even-factors of $n$. Therefore, the number of ways to express any positive number $n$ equals the number of odd factors of $n$

 

[fresh_42]

Thanks to @fresh_42 for the hint! The answer is too obvious after that. I merely add some formalism for the sake of completeness. Before my earlier attempt, I had briefly considered working backward from the formula for sum of sequence as suggested by the hint but didn't proceed along that line as I thought I could arrive at a more "intuitive" solution that didn't need formulae, and that made giving a proof more complex that needed.

(11. Show that the number of ways to express a positive integer $n$ as the sum of consecutive positive integers is equal to the number of odd factors of $n$.)

Spoiler: Question 11

Any sequence of $k$ consecutive integers can be written as $a+1, a+2, ..., a+k$. Here $a+1$ is the 1st integer in the sequence. The sum of this sequence is $ka + \frac {k(k+1)} {2} = k(a + \frac {k+1} {2})$. We consider positive integer values for $k$, i.e. $k \in \{2, 3, 4, .., \}$ (since $k$ is the length of a non-empty sequence, it must be a positive integer). We ignore $k=1$ as that will correspond to the degenerate case of single-element sequence $(n)$, whereas the question apparently considers only sequences having more than 1 integer (except when $n$ itself is 1, in which case there is exactly one sequence satisfying the criteria, $\{1\}$).

• We inspect values of $k \in \{2, 3, .., \}$ and look for the value of $a$ such that the sum of the sequence $a+1, a+2, .., a+k$ sums to $n$, i.e. $$k(a + \frac {k+1} {2}) = n$$.
• If $k$ is NOT a factor of $n$, then $(a + \frac {k+1} {2})$ would be non-integer in the above equation, implying that there is no integer $a$ such that a $k$-length integer sequence will add up to $n$, so we only need to consider those values of $k$ that are factors of $n$.
• If $k$ is even, then $\frac {k+1} {2}$ would be a non-integer, so again (even if that $k$ is a factor of $n$), there would be no $k$-length integer sequence that adds up to $n$
• If $k$ is an odd factor of $n$, then $\frac {k+1} {2}$ is an integer and we can find an integer value for $a$ such that the $k$-long sequence starting at $a+1$ adds up to $n$. $a$ is given by the equation $$a = \frac {n} {k} - \frac {k+1} {2}$$
• The value of $a$ from the above equation could be negative, whereas we want only sequences that consist of positive integers alone. It is easy to show that any integer sequence $a+1, a+2, .. a+k$ that adds up to a positive value can be reduced to a positive integer sub-sequence if the original sequence starts with zero or a negative integer
  • If the sequence starts with 0, will simply drop that as removing 0 does not alter the sum of the sequence​
  • If the sequence starts with a negative number and yet adds up to a positive number, then it must be the case that the sequence is of the form $-x, -x+1, -x+2, ..., 0, 1, .., x, x+1, .., x+j$ (for some positive integers $x, j$ satisfying the condition $x = -(a+1)$, $x+j = (a+k)$), i.e. for every negative integer $-y$, the sequence should also contain the positive integer $y$ and the number of positive integers in the sequence should exceed the number of negative integers in the sequence. In effect, the negative integers get canceled out by their positive counterparts in the summation, so we can trim a left portion of original sequence and get a positive-integers-only sequence ($(x+1, x+2, ..., x+j)$) that adds up to the same value as the original sequence.​

Thus, for every odd-factor $k$ of $n$, we can find a unique sequence of consecutive positive integers that sum to $n$ whereas no such sequence would exist for even-factors of $n$. Therefore, the number of ways to express any positive number $n$ equals the number of odd factors of $n$

Thus, for every odd-factor $k$ of $n$, we can find a unique sequence of consecutive positive integers that sum to $n$

Where did you show uniqueness?

O.k., it's still too excessive$^*)$ but shows that we get a partition from odd factors. Now couldn't it be, that two factors lead to the same partition, in which case our correspondence wouldn't be one-to-one?

$^*)$ My suggestion had been $2n=2(r+(r+1)+\ldots +(r+k))=(k+1)(2r+k)$ where exactly one factor is odd. Hence an odd factor belongs to a partition. But this doesn't show uniqueness either, which requires a bit more work to do.

 

[Not anonymous]

Where did you show uniqueness?

O.k., it's still too excessive$^*)$ but shows that we get a partition from odd factors. Now couldn't it be, that two factors lead to the same partition, in which case our correspondence wouldn't be one-to-one?

$^*)$ My suggestion had been $2n=2(r+(r+1)+\ldots +(r+k))=(k+1)(2r+k)$ where exactly one factor is odd. Hence an odd factor belongs to a partition. But this doesn't show uniqueness either, which requires a bit more work to do.

To show the uniqueness of the sequence for any given value of $k$, we first show the uniqueness of $a$ given $k$. Suppose 2 different values of $k$ , say $k_1$ and $k_2$ led to the same of $a$, then it must be the case where $\frac n {k_1} − \frac {k_1+1} {2} = \frac n {k_2} − \frac {k_2+1} {2} \implies \frac n {k_1 k_2} = - \frac 1 2 \implies k_1 k_2 = -2n$. That would require either $k_1$ or $k_2$ to be negative, but since only positive values of $k$ are to be considered, no 2 distinct valid values of $k_1$ and $k_2$ will meet that condition required to yield the same value for $a$. And 2 distinct values of $a$ will result in 2 distinct "untrimmed" sequences, as $a+1$ is the 1st integer in the untrimmed sequences. Since trimming is no done if the original sequnce started at a positive number, 2 distinct positive values of $a$ will continue to be map to 2 distinct sequences.

The other thing to be proven is that even when $a$ is negative, the "trimmed" sequence will be distinct from other valid sequences that sum to $n$.

• If we consider two different negative values of $a$, $a_1$ and $a_2$. As shown earlier, the corresponding "trimmed" sequences should start at $-(a_1 + 1) +1 = -a_1$ and $-(a_2 + 1) +1 = -a_2$ respectively and those should be distinct from each other if $a_1$ and $a_2$ are distinct.
• If we consider a positive value $a_1$ (corresponding to $k = k_1$) and a negative value $a_2$ (corresponding to $k = k_2$) o $a$. The earlier proof already showed that only odd factors of $k$ can yield valid sequences, so any original "untrimmed" sequence must have an odd number of integers. Now trimming is done only when $a$ is negative, and when it is done, an odd number of elements are removed from the sequence (every negative number $-x$ in the original sequence is canceled out by the corresponding positive number $x$, resulting in an even number of positive and negative values getting removed and then number 0 is also removed, so in total an odd number of values get removed). More formally, for the negative value $a_2$, we end up removing $-2(a_1 + 1) +1$ numbers from the sequence, and that count is an odd number. When an odd number of elements are removed from an original sequence containing an odd number, the resulting sequence will have an even number of elements. Thus a sequence that originally started at a negative integer $a_2$ will be trimmed to an even-length sequence, whereas a sequence that originally started as a positive integer $a_1$ will continue to remain an odd-length sequence as it does not get trimmed. Hence the two sequences must be distinct.

 

[fresh_42]

Hence the two sequences must be distinct.

You are not easy to follow. I think you should practice to strip unnecessary explanations in proofs and concentrate more on small logical steps. "should" isn't really appropriate to appear in a proof. Maybe this little article https://www.physicsforums.com/insights/how-most-proofs-are-structured-and-how-to-write-them/ can help, but I'm not sure. I have written better ones than this. So this example here is perhaps a better way to say what I meant:

We still have $2n=(k+1)(2r+k)=2(r+\ldots +(r+k))$ as partition for $n$. The crucial part is to note, that this splits into factors with exactly one of them is odd, hence we can directly compare the factors of:

If we have two decompositions $2n=(k+1)(2r+k)=(l+1)(2s+l)$ and $k+1=l+1$ or $2r+k=2s+l$ are the same odd numbers, then $k=l$ in both cases. If we have $k+1=2s+l$ then $l+1=k+2-2s=\dfrac{2n}{2s+l}=2r+k$ and $r=1-s$ or $r,s\in \{\,0,1\,\}$. For $(r,s)=(0,1)$ we get $2n=(k+1)k=(l+1)(k+1)$ or $k=l+1$, and for $(r,s)=(1,0)$ we have $2n=(l+1)l=l(2+k)$ or $l=k+1$ which is again the same odd factor as $2n=(l+2)(l+1)=(k+1)(k+2)$ is the same decomposition.

 

[archaic]

Spoiler: Speculating on question 15

These are speculations, I can't really answer the question.
$$
S = \int_{\frac{1}{2}}^{3} \dfrac{1}{\sqrt{x^2+1}}\,\dfrac{\log(x)}{\sqrt{x}}\,dx \, + \, \int_{\frac{1}{3}}^{2} \dfrac{1}{\sqrt{x^2+1}}\,\dfrac{\log(x)}{\sqrt{x}}\,dx\\
= \int_{\frac{1}{3}}^{3} \dfrac{1}{\sqrt{x^2+1}}\,\dfrac{\log(x)}{\sqrt{x}}\,dx+\int_{\frac{1}{2}}^{2} \dfrac{1}{\sqrt{x^2+1}}\,\dfrac{\log(x)}{\sqrt{x}}\,dx
$$
This seemed to be equal to zero so I tried computing the area using some triangles and rectangles. I think that it's because of the fact that $\log{\frac{1}{a}}+\log{a}=0$ or something like this.