reignofdragons
- 3
- 0
On a bright sunny day, two girls play tug of war while standing on the opposite sides of a pond. Initially, each stands at a distance d from her edge of the pond. Jackie, who weighs less than her opponent Sue, loses the tug of war and is forced to take a dive in the pond. (Most often, the tug of war is won by the heaviest, not the strongest, team--you will find out why when you learn more about friction.)
Jackie's mass is m, the tension in the rope is T, and the opposing force of friction between Jackie's feet and the ground is f.
Find the time Delta t it took Sue to win the competition.
Things i figured out that are correct for sure:
--Jackie can be treated as a particle moving with constant nonzero acceleration.
--Which of the following assumptions or interpretations are reasonable?
1. Air resistance is substantial.
2. Air resistance is negligible.
3. The ground near the pond is slanted toward the water.
4. The ground near the pond is horizontal.
5. The mass of the rope equals Jackie's mass.
6. The mass of the rope is negligible.
7. The rope is unstretchable.
--Based on your motion diagram, which statements about Jackie's vertical acceleration \vec a_y must be true?
1. The magnitude of \vec a_y is greater than that of \vec a_x.
2. The magnitude of \vec a_y is zero.
3. The magnitude of \vec a_y is infinitely large.
4. \vec a_y is directed downward.
5. \vec a_y is directed upward.
Now the part i can't seem to grasp the concept, any help is appreciated.
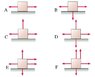
Assuming that in the tug of war Jackie is being pulled to the right, which of the free-body diagrams shown is correct?
Note that the forces are not drawn to scale. Also, they are not labeled; however, they should be labeled on your own diagram.
look at attached photo for above question
Look at your pictorial representation. Which of the following are known quantities in this problem?
1. Jackie's initial horizontal position
2. The distance Jackie is pulled before reaching the edge of the pond
3. Jackie's horizontal acceleration
4. Jackie's initial horizontal velocity
5. Jackie's horizontal velocity at the moment she reaches the edge of the pond
6. The time it takes for Sue to pull Jackie into the pond
Thanks for your time and help.
Jackie's mass is m, the tension in the rope is T, and the opposing force of friction between Jackie's feet and the ground is f.
Find the time Delta t it took Sue to win the competition.
Things i figured out that are correct for sure:
--Jackie can be treated as a particle moving with constant nonzero acceleration.
--Which of the following assumptions or interpretations are reasonable?
1. Air resistance is substantial.
2. Air resistance is negligible.
3. The ground near the pond is slanted toward the water.
4. The ground near the pond is horizontal.
5. The mass of the rope equals Jackie's mass.
6. The mass of the rope is negligible.
7. The rope is unstretchable.
--Based on your motion diagram, which statements about Jackie's vertical acceleration \vec a_y must be true?
1. The magnitude of \vec a_y is greater than that of \vec a_x.
2. The magnitude of \vec a_y is zero.
3. The magnitude of \vec a_y is infinitely large.
4. \vec a_y is directed downward.
5. \vec a_y is directed upward.
Now the part i can't seem to grasp the concept, any help is appreciated.
Assuming that in the tug of war Jackie is being pulled to the right, which of the free-body diagrams shown is correct?
Note that the forces are not drawn to scale. Also, they are not labeled; however, they should be labeled on your own diagram.
look at attached photo for above question
Look at your pictorial representation. Which of the following are known quantities in this problem?
1. Jackie's initial horizontal position
2. The distance Jackie is pulled before reaching the edge of the pond
3. Jackie's horizontal acceleration
4. Jackie's initial horizontal velocity
5. Jackie's horizontal velocity at the moment she reaches the edge of the pond
6. The time it takes for Sue to pull Jackie into the pond
Thanks for your time and help.