Solving Two Masses 3 Springs Homework Problem

[MMS]

Homework Statement
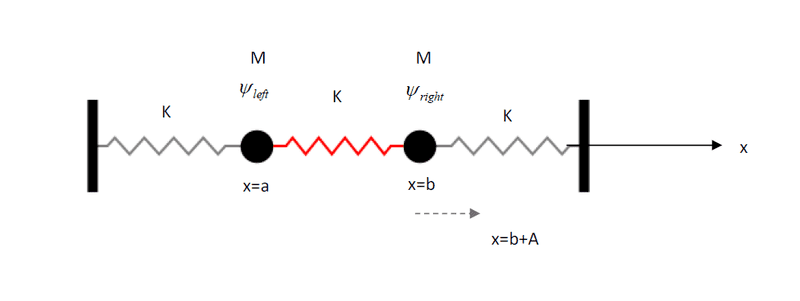
Given: Two masses M between 3 springs of constant K. equilibrium point for the left mass is x=a, for the right one x=b. We move the right mass to point x=b+A

1. What is the return force?
2. What is the work required to create the initial condition?
3. Can we write the energy of the system as: E=(1/2)*M*((w1)^2)*(A/2)^2+(1/2)*M*((w2)^2)*(A/2)^2 ?
4. Is there a time where Ψleft=A

The attempt at a solution

I'm currently stuck on 1 and it's pretty much confusing me but here is what I thought of:

The net force on each mass is the return force (for each).

For the left mass:
Well the left spring isn't affected at all since there is no displacement in it's position, therefore the only thing that this mass feels is K*A to the right.
Therefore, the return force is: F=K*A(x^^), x^^=x(hat)

For the right mass:
It feels to the right a force of -KA and to the left a force of KA. Summing those up with the right directions gives us a return force of F=-2K*A (x^^), x^^=x(hat)

All this, while taking into consideration that there is no displacement in the left mass.

To be honest I'm not quite sure if what I defined as the return force is actually the return force so I'd love some help with that as well.Any help is much appreciated. Thank you.

 

[haruspex]

It's not clear, but I suspect that you are supposed to assume the left mass moves so as to stay in equilibrium. (Otherwise it seems rather irrelevant - it might as well be a wall.)

 

[Simon Bridge]

That's how I'm reading it: you grab mass B (equilibrium position x=b), move it to a new position, and hold it there: what happens?
The questions step you through some of the consequences.

The way the problem is set out suggests that you have an example of this sort of calculation in your notes somewhere.

 

[MMS]

It's not clear, but I suspect that you are supposed to assume the left mass moves so as to stay in equilibrium. (Otherwise it seems rather irrelevant - it might as well be a wall.)

I asked the tutor about whether there is movement due to to the displacement of the right mass and his answer was that we only move a single mass.

 

[MMS]

That's how I'm reading it: you grab mass B (equilibrium position x=b), move it to a new position, and hold it there: what happens?
The questions step you through some of the consequences.

The way the problem is set out suggests that you have an example of this sort of calculation in your notes somewhere.

We have the classic example where there is displacement in both masses. Can I simply think of the equations as the same ones where Ψ of the other mass is simply 0?

Also, you guys didn't tell me if what I stated is actually the return force because I'm not too sure about that (or if someone could define it properly here I'd also appreciate it).Thanks for the replies guys.

 

[haruspex]

Still struggling to understand the complete statement of the problem. From part 4, it appears there is some dynamic aspect. My next guess is:
RH mass is moved A to the right while the LH mass is held still; both masses are then released.
If so, part 1 is asking for the return force (on RH mass, presumably) before release.

It feels to the right a force of -KA and to the left a force of KA.

Strictly speaking, there may be a tension T in the springs at equilibrium, so when displaced each tension may be T more than you say. But these will cancel out.

Summing those up with the right directions gives us a return force of F=-2K*A (x^^), x^^=x(hat)

$\hat x$? Are you generalising the displacement from the initial A to $\hat x = \hat x(t)$, and a force of $-2K \hat x$? If so, I agree.

 

[Simon Bridge]

I asked the tutor about whether there is movement due to to the displacement of the right mass and his answer was that we only move a single mass.

... well in that case the initial condition is that the left mass is held at x=a, and the right mass is now held at x=b+A.
i.e. the left mass is just a wall - until the masses are released.
But:

We have the classic example where there is displacement in both masses.

... this would contradict what your tutor told you then. Either the left mass is displaced as a result of the displacement of the right mass or it is not.

Also, you guys didn't tell me if what I stated is actually the return force because I'm not too sure about that...

Unless you clear up the ambiguity about the movement of the masses, it is impossible to tell.
But the approach is basically correct - you sum the forces left and right.
note: a unit vector in the +x direction can be written i or i or e_x or $\hat\imath$ or $\hat x$ etc.

Can I simply think of the equations as the same ones where Ψ of the other mass is simply 0?

I cannot tell - you have yet to define Ψ.
Guessing: no - once free to move, the masses will exchange energy and momentum.

 

[MMS]

I'll reply to both of you guys.

First of all, I want to thank for the help.

Now to the main point, I agree that the way this problem was presented is quite confusing. But after looking a lot into it and using simple logic, I believe I've finally understood what is meant here.
Basically, what is going on here, the right mass is moved to the right by A from its equilibrium point as the left mass, at that moment, is still at rest. I believe by this they mean that they're simply stating an initial value to the displacement of each mass at some t. Just like both of you guys said (also, this is what seems to make most sense since they didn't state that they're holding the left mass or something).
From here, I solved for the most general case as if both masses had displacements and found the Ψ(t) for each mass (I used both F=ma and F=-kx and worked it out in a matrix). With 4 unknown constants and 4 initial values (2 for the displacement and 2 for the velocities), I was able to find the solution Ψ(t) per mass for this particular case. I took the 2nd derivative of Ψ for each mass and multiplied it by m and from there, I got two equations each indicating the return force for each mass.
I checked this answer by substituting t=0 into each equation and got the return force I expected for each mass which is pretty similar to what I stated above in the solution attempt.
I hope it's clearer now.

 

[MMS]

By the way, what I found was:

Ψleft=(A/2)*cos(sqrt(k/m)*t)+(A/2)*cos(sqrt(3k/m)*t)

Ψright=(A/2)*cos(sqrt(k/m)*t)-(A/2)*cos(sqrt(3k/m)*t)

For 2. I said that the work is the change in the energy and since there is only change in the elastic potential energy to make the system as it is described we need W=(1/2)*K*A^2

as for 3. I'm not sure how to solve it, any ideas?

 

[haruspex]

as for 3. I'm not sure how to solve it, any ideas?

What are w1 and w2?

 

[MMS]

I believe it's what I found: sqrt(k/m) and sqrt(3k/m).

 

[BvU]

For 2. I said that the work is the change in the energy and since there is only change in the elastic potential energy to make the system as it is described we need W=(1/2)*K*A^2

That is strange. To move the right mass you need to overcome the restoring force of two springs. The expression is what you get for one spring...

And if I peek ahead, the thing to prove in 3) seems to agree with that idea...

 

[haruspex]

I believe it's what I found: sqrt(k/m) and sqrt(3k/m).

I meant, how are they defined in

E=(1/2)*M*((w1)^2)*(A/2)^2+(1/2)*M*((w2)^2)*(A/2)^2

If their nature is not prescribed then it is trivially true that E can be written in that form.
From your answer I deduce they're oscillation frequencies.
I concur with BvU's post #12.