Logical Dog
- 362
- 97
Hello.
This is how every number in the decimal system is expressed:
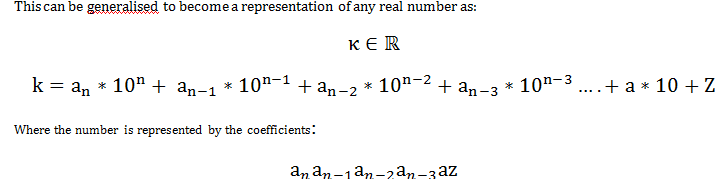
I had understood this topic earlier but as I was revising it today I have become confused somewhat.
I know that for the decimal system, we have 9 digits.
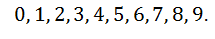
I understand this:
- When we use a base between 1-10, we do not need to come up with new digits.
- in the illustration one above, if the base is x, the coefficient a can only be less than x? Am I correct?
- I am confused as to how to divide numbers and change them to other bases, I seem to have forgotten basic division.
I understand 372 expressed in base 10 is 3*10*10 +7*10 + 2
But what I don't get is this, 372 is already expressed in base 10 when we divide it by 10?
I am really confused. All numbers are intuitively expressed in base 10 before we convert them to other bases..but division by the same base in the same form seems to give the same number.
This is how every number in the decimal system is expressed:
I had understood this topic earlier but as I was revising it today I have become confused somewhat.
I know that for the decimal system, we have 9 digits.
I understand this:
- When we use a base between 1-10, we do not need to come up with new digits.
- in the illustration one above, if the base is x, the coefficient a can only be less than x? Am I correct?
- I am confused as to how to divide numbers and change them to other bases, I seem to have forgotten basic division.
I understand 372 expressed in base 10 is 3*10*10 +7*10 + 2
But what I don't get is this, 372 is already expressed in base 10 when we divide it by 10?
I am really confused. All numbers are intuitively expressed in base 10 before we convert them to other bases..but division by the same base in the same form seems to give the same number.