Sound problem: Destructive Interference

[coconutgt]

The drawing shows a loudspeaker A and point C, where a listeer is positioned. A second loudspeaker B is located somewhere to the right of A. Both speakers vibrate in phase and are playing a 68.6-Hz tone. The speed of sound is 343 m/s. What is the closest to speaker A that speaker B can be located, so that the listener hears no sound?

Picture:

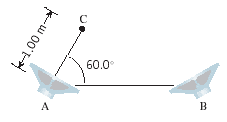
First, I connected C and B to make a triangle. I then bisect the triangle with a line straight down from C to make 2 triangles (with the extra point being D). I call AB line = x and CD line = y. Next, I set up the destructive interference where the point in which line AB has to be 1 wavelength and line CB is half wavelength. So, the difference between AC and CB has to be

CB - CA = (n*wavelength)/2

for smallest distance, n would have to be 1.

with this, I list all the known and unknowns which are

AD = AC*cos(60)
DB = AB-AD -> x-cos(60)
CD = AC*sin(60)

CB = sqrt(sin^2(60)+ (x-cos^2(60)))

So then:

wavelength/2 = sqrt(sin^2(60)+cos^2(60) + x^2 - 2*cos(60x))

I solve to get:

x^2 - (2*cos(60)x) + (1 + wavelength^2/4)


use quadratic equation to get

x = 2.845 and x = -1.845

The correct answer is 3.89 m.

So, I don't know if I'm missing something here. I hope you guys can help. Thanks.

 

[OlderDan]

I can't say I followed all of your trig, but it looks to me like you said

CB = sqrt(sin^2(60)+ (x-cos^2(60))) = wavelength/2 = sqrt(sin^2(60)+cos^2(60) + x^2 - 2*cos(60x))

and that is not true

CB = CA + wavelength/2

You might consider using the Law of Sines to do this problem. CB is easy to find and you know angle CAB = 60°. Finding angle CBA and then angle ACB is easier with LoS than what you did.