Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading Andrew Browder's book: "Mathematical Analysis: An Introduction" ... ...
I am currently reading Chapter 12: Multilinear Algebra ... ...
I need some help in order to fully understand the proof of Theorem 12.22 on page 276 ... ...The relevant text reads as follows:
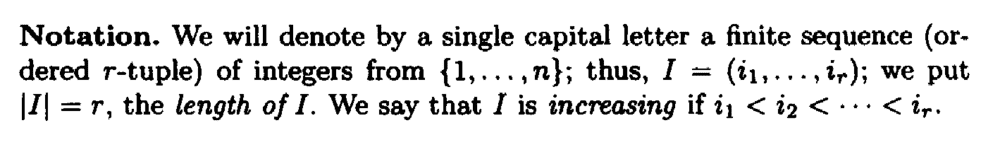

In the above proof by Browder we read the following:
" ... ... the Kronecker delta, and hence, using Proposition 12.20, that for any ##r##-tuples ##I## and ##J##, not necessarily increasing
##\tilde{u}^I ( u_{ j_1 }, \cdot \cdot \cdot u_{ j_r } ) = \varepsilon^I_J##
where ##\varepsilon^I_J##, the "Kronecker epsilon" ... ... "My question is as follows:
How is Proposition 12.20 used to show that ## \tilde{u}^I ( u_{ j_1 }, \cdot \cdot \cdot u_{ j_r } ) = \varepsilon^I_J## ... ... could someone please demonstrate the use of Proposition 12.20 to derive this result ...The above proof refers to Proposition 12.20 so I am providing the text of this proposition as follows:

The above proof also refers (indirectly) to the basis ##( \tilde{u}^1, \cdot \cdot \cdot \tilde{u}^n )## for the dual space ##V^*## ... ... this is mentioned at the start of Section 12.1 ... so I am providing the relevant text as follows:




It may also be useful in order to understand the above post for Physics Forum members to have access to Section 12.2 on Alternating Tensors ... so I am providing the same as follows:



 Hope access to the above text helps ...
Hope access to the above text helps ...
Peter
I am currently reading Chapter 12: Multilinear Algebra ... ...
I need some help in order to fully understand the proof of Theorem 12.22 on page 276 ... ...The relevant text reads as follows:
In the above proof by Browder we read the following:
" ... ... the Kronecker delta, and hence, using Proposition 12.20, that for any ##r##-tuples ##I## and ##J##, not necessarily increasing
##\tilde{u}^I ( u_{ j_1 }, \cdot \cdot \cdot u_{ j_r } ) = \varepsilon^I_J##
where ##\varepsilon^I_J##, the "Kronecker epsilon" ... ... "My question is as follows:
How is Proposition 12.20 used to show that ## \tilde{u}^I ( u_{ j_1 }, \cdot \cdot \cdot u_{ j_r } ) = \varepsilon^I_J## ... ... could someone please demonstrate the use of Proposition 12.20 to derive this result ...The above proof refers to Proposition 12.20 so I am providing the text of this proposition as follows:
The above proof also refers (indirectly) to the basis ##( \tilde{u}^1, \cdot \cdot \cdot \tilde{u}^n )## for the dual space ##V^*## ... ... this is mentioned at the start of Section 12.1 ... so I am providing the relevant text as follows:
It may also be useful in order to understand the above post for Physics Forum members to have access to Section 12.2 on Alternating Tensors ... so I am providing the same as follows:
Peter
Attachments
-
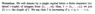 Browder - 1 - Proposition 12.22 ... ... PART 1 ... .png13.8 KB · Views: 369
Browder - 1 - Proposition 12.22 ... ... PART 1 ... .png13.8 KB · Views: 369 -
 Browder - 2 - Proposition 12.22 ... ... PART 2 ... ... .png49.6 KB · Views: 429
Browder - 2 - Proposition 12.22 ... ... PART 2 ... ... .png49.6 KB · Views: 429 -
 Browder ... Proposition 12.20 ... .png44.8 KB · Views: 396
Browder ... Proposition 12.20 ... .png44.8 KB · Views: 396 -
 Browder - 1 - Start of Chapter 12 ... ... PART 1.png75.6 KB · Views: 398
Browder - 1 - Start of Chapter 12 ... ... PART 1.png75.6 KB · Views: 398 -
 Browder - 2 - Start of Chapter 12 ... ... PART 2 .png59.5 KB · Views: 396
Browder - 2 - Start of Chapter 12 ... ... PART 2 .png59.5 KB · Views: 396 -
 Browder - 3 - Start of Chapter 12 ... ... PART 3 .png51.6 KB · Views: 393
Browder - 3 - Start of Chapter 12 ... ... PART 3 .png51.6 KB · Views: 393 -
 Browder - 3 - Start of Chapter 12 ... ... PART 3 .png51.6 KB · Views: 379
Browder - 3 - Start of Chapter 12 ... ... PART 3 .png51.6 KB · Views: 379 -
 Browder - 4 - Start of Chapter 12 ... ... PART 4 .png49.2 KB · Views: 367
Browder - 4 - Start of Chapter 12 ... ... PART 4 .png49.2 KB · Views: 367 -
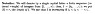 ?temp_hash=2efdb9106079a85a3568e58731f43740.png13.8 KB · Views: 631
?temp_hash=2efdb9106079a85a3568e58731f43740.png13.8 KB · Views: 631 -
 ?temp_hash=2efdb9106079a85a3568e58731f43740.png49.6 KB · Views: 712
?temp_hash=2efdb9106079a85a3568e58731f43740.png49.6 KB · Views: 712 -
 ?temp_hash=2efdb9106079a85a3568e58731f43740.png44.8 KB · Views: 751
?temp_hash=2efdb9106079a85a3568e58731f43740.png44.8 KB · Views: 751 -
 ?temp_hash=2efdb9106079a85a3568e58731f43740.png75.6 KB · Views: 635
?temp_hash=2efdb9106079a85a3568e58731f43740.png75.6 KB · Views: 635 -
 ?temp_hash=2efdb9106079a85a3568e58731f43740.png59.5 KB · Views: 612
?temp_hash=2efdb9106079a85a3568e58731f43740.png59.5 KB · Views: 612 -
 ?temp_hash=2efdb9106079a85a3568e58731f43740.png51.6 KB · Views: 617
?temp_hash=2efdb9106079a85a3568e58731f43740.png51.6 KB · Views: 617 -
 ?temp_hash=2efdb9106079a85a3568e58731f43740.png49.2 KB · Views: 616
?temp_hash=2efdb9106079a85a3568e58731f43740.png49.2 KB · Views: 616 -
 Browder - 1 - Start of Section 12.2 ... ... PART 1 .... .png53.8 KB · Views: 433
Browder - 1 - Start of Section 12.2 ... ... PART 1 .... .png53.8 KB · Views: 433 -
 Browder - 2 - Start of Section 12.2 ... ... PART 2 .... .png36.4 KB · Views: 375
Browder - 2 - Start of Section 12.2 ... ... PART 2 .... .png36.4 KB · Views: 375 -
 Browder - 3 - Start of Section 12.2 ... ... PART 3 .... .png53.2 KB · Views: 400
Browder - 3 - Start of Section 12.2 ... ... PART 3 .... .png53.2 KB · Views: 400 -
 Browder - 3 - Start of Section 12.2 ... ... PART 3 .... .png53.2 KB · Views: 374
Browder - 3 - Start of Section 12.2 ... ... PART 3 .... .png53.2 KB · Views: 374 -
 Browder - 4 - Start of Section 12.2 ... ... PART 4 .... .png41.8 KB · Views: 385
Browder - 4 - Start of Section 12.2 ... ... PART 4 .... .png41.8 KB · Views: 385 -
 ?temp_hash=2932f319424fbb980ad6d60a210b478c.png53.8 KB · Views: 665
?temp_hash=2932f319424fbb980ad6d60a210b478c.png53.8 KB · Views: 665 -
 ?temp_hash=2932f319424fbb980ad6d60a210b478c.png36.4 KB · Views: 648
?temp_hash=2932f319424fbb980ad6d60a210b478c.png36.4 KB · Views: 648 -
 ?temp_hash=2932f319424fbb980ad6d60a210b478c.png53.2 KB · Views: 602
?temp_hash=2932f319424fbb980ad6d60a210b478c.png53.2 KB · Views: 602 -
 ?temp_hash=2932f319424fbb980ad6d60a210b478c.png41.8 KB · Views: 621
?temp_hash=2932f319424fbb980ad6d60a210b478c.png41.8 KB · Views: 621
Last edited: