Space of Alternating Tensors of Rank r.... (Browder, 12.22)

[Math Amateur]

I am reading Andrew Browder's book: "Mathematical Analysis: An Introduction" ... ...

I am currently reading Chapter 12: Multilinear Algebra ... ...

I need some help in order to fully understand the proof of Theorem 12.22 on page 276 ... ...The relevant text reads as follows:

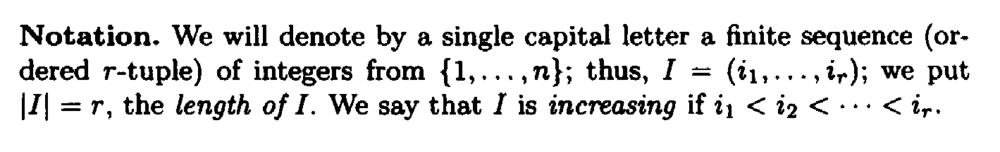
In the above proof by Browder we read the following:

" ... ... the Kronecker delta, and hence, using Proposition 12.20, that for any $r$-tuples $I$ and $J$, not necessarily increasing

$\tilde{u}^I ( u_{ j_1 }, \cdot \cdot \cdot u_{ j_r } ) = \varepsilon^I_J$

where $\varepsilon^I_J$, the "Kronecker epsilon" ... ... "My question is as follows:

How is Proposition 12.20 used to show that $\tilde{u}^I ( u_{ j_1 }, \cdot \cdot \cdot u_{ j_r } ) = \varepsilon^I_J$ ... ... could someone please demonstrate the use of Proposition 12.20 to derive this result ...The above proof refers to Proposition 12.20 so I am providing the text of this proposition as follows:

The above proof also refers (indirectly) to the basis $( \tilde{u}^1, \cdot \cdot \cdot \tilde{u}^n )$ for the dual space $V^*$ ... ... this is mentioned at the start of Section 12.1 ... so I am providing the relevant text as follows:

It may also be useful in order to understand the above post for Physics Forum members to have access to Section 12.2 on Alternating Tensors ... so I am providing the same as follows:

Hope access to the above text helps ...

Peter

 

[WWGD]

I suggest you narrow this to a few lines to make it more likely someone will read the whole thing. Please summarize it for us, the parts you don't understand.

 

[Math Amateur]

I suggest you narrow this to a few lines to make it more likely someone will read the whole thing. Please summarize it for us, the parts you don't understand.

Hi WWGD ... thanks for the response ...

Almost all of the scanned text in my post is to enable readers to check definitions and notation (only if they need to ...) ... it is not necessary for a reader who knows the topic to read all the text ... maybe just to check the meaning of notation every now and then ..

The essence of my problem is one of the early steps in the proof of the following proposition in Browder's book:

12.22 Proposition The set

$\{ \tilde{u}^I \ : \ \mid I \mid = r, \ I \text{ increasing } \}$

forms a basis for $\bigwedge^r ( V^* )$Now the proof starts by noting that ...

... ... if $I = ( i_1, \cdot \cdot \cdot , i_r )$ and $J = ( j_1, \cdot \cdot \cdot , j_r )$ are increasing sequences then $\tilde{u}^I (u_{ j_1}, \cdot \cdot \cdot , u_{ j_r} ) = A ( \tilde{u}^{i_1} \otimes \cdot \cdot \cdot \otimes \tilde{u}^{i_r} ) ( u_{j_1} \ ... \ u_{j_r} )$$= \sum_{ \sigma \text{ in } S_r } \varepsilon ( \sigma ) \tilde{u}^{i_1} \otimes \cdot \cdot \cdot \otimes \tilde{u}^{i_r} ( u_{j_{\sigma (1) } } \ ... \ u_{j_{\sigma (r) } } )$$= \delta^I_J$

The proof then notes that it follows that for any $r$-tuples $I$ and $J$, not necessarily increasing,

$\tilde{u}^I ( u_{ j_1 }, \cdot \cdot \cdot u_{ j_r } ) = \varepsilon^I_J$

where $\varepsilon^I_J$, the "Kronecker epsilon" is defined to be $0$ unless the sequence $I$ is a rearrangement of the sequence $J$, and to be $\varepsilon ( \sigma )$, if the permutation $\sigma$ transforms $I$ to $J$. ... ...My question is as follows:

How/why does it follow that for any $r$-tuples $I$ and $J$, not necessarily increasing,

$\tilde{u}^I ( u_{ j_1 }, \cdot \cdot \cdot u_{ j_r } ) = \varepsilon^I_J$ ... ... ?

Indeed ... can someone please demonstrate that it follows that $\tilde{u}^I ( u_{ j_1 }, \cdot \cdot \cdot u_{ j_r } ) = \varepsilon^I_J$ ...(NOTE: Browder says using Proposition 12.20 it follows that ,,, ,,, etc etc ... )Help will be much appreciated ...

Peter

.

 

[fresh_42]

Hi Peter,

you have a strange favor for books with exhausting notations.

I assume $\tilde{u}^i(u_j) \stackrel{(*)}{=} \delta_{ij}$ and that $(\tilde{u}^{i_1}\otimes \tilde{u}^{i_2})(u_{j_1}\, , \,u_{j_2}) = \tilde{u}^{i_1}(u_{j_1}) \cdot \tilde{u}^{i_2}(u_{j_2})\,.$ With this it is probably easiest if you write out the sums for $r=2$ and $r=3$ and you will see what is going on. The sum over the permutations is the definition of the alternator $A$. Increasing $I$, resp. $J$, can always be achieved from arbitrary ones by consecutively swapping indices and multiplying with $(-1)$ for every swap which is made: $A(a\otimes b) = -A(b \otimes a)$. Because of $(*)$ it is sufficient to order $I$ since only those terms $\tilde{u}^{i}(u_{j})$ will remain unequal to zero which fit to the same ordering as $I$.

 

[Math Amateur]

Hi Peter,

you have a strange favor for books with exhausting notations.

I assume $\tilde{u}^i(u_j) \stackrel{(*)}{=} \delta_{ij}$ and that $(\tilde{u}^{i_1}\otimes \tilde{u}^{i_2})(u_{j_1}\, , \,u_{j_2}) = \tilde{u}^{i_1}(u_{j_1}) \cdot \tilde{u}^{i_2}(u_{j_2})\,.$ With this it is probably easiest if you write out the sums for $r=2$ and $r=3$ and you will see what is going on. The sum over the permutations is the definition of the alternator $A$. Increasing $I$, resp. $J$, can always be achieved from arbitrary ones by consecutively swapping indices and multiplying with $(-1)$ for every swap which is made: $A(a\otimes b) = -A(b \otimes a)$. Because of $(*)$ it is sufficient to order $I$ since only those terms $\tilde{u}^{i}(u_{j})$ will remain unequal to zero which fit to the same ordering as $I$.

Thanks fresh_42 for a most helpful post ...

You write: " ... ... I assume $\tilde{u}^i(u_j) \stackrel{(*)}{=} \delta_{ij}$ and that $(\tilde{u}^{i_1}\otimes \tilde{u}^{i_2})(u_{j_1}\, , \,u_{j_2}) = \tilde{u}^{i_1}(u_{j_1}) \cdot \tilde{u}^{i_2}(u_{j_2})\,.$ ... " ... ... yes, that is my understanding ...You also write: " ... ... With this it is probably easiest if you write out the sums for $r=2$ and $r=3$ and you will see what is going on. ... " ... ... Good idea ... thanks ...I have been reflecting on the issues and although the result that $\tilde{u}^I ( u_{ j_1 }, \cdot \cdot \cdot u_{ j_r } ) = \varepsilon^I_J$ now seems reasonable to me ... how/why Proposition 12.20 is involved in establishing this result is a mystery to me ... are you able to help ..?
Another worry I have is that it seems to me that it is quite possible for some terms in the expression

$= \sum_{ \sigma \text{ in } S_r } \varepsilon ( \sigma ) \tilde{u}^{i_1} \otimes \cdot \cdot \cdot \otimes \tilde{u}^{i_r} ( u_{j_{\sigma (1) } } \ ... \ u_{j_{\sigma (r) } } )$

to be $-1$ as surely for some permutations $\sigma$ we will have $\varepsilon ( \sigma ) = -1$ ...

... ... but ... ... this surely might possibly mean

$\tilde{u}^I (u_{ j_1}, \cdot \cdot \cdot , u_{ j_r} ) \neq \delta^I_J$ ... ... can you clarify ...?Thanks again for your help... it is much appreciated ...

Peter

 

[fresh_42]

I have been reflecting on the issues and although the result that $\tilde{u}^I ( u_{ j_1 }, \cdot \cdot \cdot u_{ j_r } ) = \varepsilon^I_J$ now seems reasonable to me ... how/why Proposition 12.20 is involved in establishing this result is a mystery to me ... are you able to help ..?

Proposition 12.20 only says which properties the alternator has - and again in a far too complicated manner. Especially $A(a\otimes b) = a\otimes b - b \otimes a = -A(b\otimes a)$ is frequently needed in order to count for the minus signs of odd permutations (as in my case $\operatorname{sgn}(b,a)=-1$).

It all comes down to the definition:
$A(\tilde{u}^{i_1}\otimes \ldots \otimes \tilde{u}^{i_r}) = \sum_{\sigma \in S_r} \varepsilon(\sigma) \tilde{u}^{\sigma(i_1)}\otimes \ldots \otimes \tilde{u}^{\sigma(i_r)}$ the sum over all possible orders of the $\tilde{u}^{i}$ weighted by the sign of their ordering. (Cp. https://en.wikipedia.org/wiki/Exterior_algebra#Alternating_multilinear_forms)

Another worry I have is that it seems to me that it is quite possible for some terms in the expression

$= \sum_{ \sigma \text{ in } S_r } \varepsilon ( \sigma ) \tilde{u}^{i_1} \otimes \cdot \cdot \cdot \otimes \tilde{u}^{i_r} ( u_{j_{\sigma (1) } } \ ... \ u_{j_{\sigma (r) } } )$

to be $-1$ as surely for some permutations $\sigma$ we will have $\varepsilon ( \sigma ) = -1$ ...

... ... but ... ... this surely might possibly mean

$\tilde{u}^I (u_{ j_1}, \cdot \cdot \cdot , u_{ j_r} ) \neq \delta^I_J$ ... ... can you clarify ...?

We have $(\tilde{u}^{i_1}\otimes \tilde{u}^{i_2})(u_{j_1}\, , \,u_{j_2}) = \tilde{u}^{i_1}(u_{j_1}) \cdot \tilde{u}^{i_2}(u_{j_2})= \delta_{i_1j_1} \cdot \delta_{i_2j_2}$ so only the pair $(i_1,i_2)=(j_1,j_2)$ remains as $\tilde{u}^i(u_j)=0$ for $i\neq j$. This is because (which I assume) $\{\,\tilde{u}^i\,\}$ and $\{\,u_j\,\}$ are dual bases of $V^*$ resp. $V$. All permutations other than the one given by $I$ vanish, esp. all odd ones.

 

[Math Amateur]

Proposition 12.20 only says which properties the alternator has - and again in a far too complicated manner. Especially $A(a\otimes b) = a\otimes b - b \otimes a = -A(b\otimes a)$ is frequently needed in order to count for the minus signs of odd permutations (as in my case $\operatorname{sgn}(b,a)=-1$).

It all comes down to the definition:
$A(\tilde{u}^{i_1}\otimes \ldots \otimes \tilde{u}^{i_r}) = \sum_{\sigma \in S_r} \varepsilon(\sigma) \tilde{u}^{\sigma(i_1)}\otimes \ldots \otimes \tilde{u}^{\sigma(i_r)}$ the sum over all possible orders of the $\tilde{u}^{i}$ weighted by the sign of their ordering. (Cp. https://en.wikipedia.org/wiki/Exterior_algebra#Alternating_multilinear_forms)

We have $(\tilde{u}^{i_1}\otimes \tilde{u}^{i_2})(u_{j_1}\, , \,u_{j_2}) = \tilde{u}^{i_1}(u_{j_1}) \cdot \tilde{u}^{i_2}(u_{j_2})= \delta_{i_1j_1} \cdot \delta_{i_2j_2}$ so only the pair $(i_1,i_2)=(j_1,j_2)$ remains as $\tilde{u}^i(u_j)=0$ for $i\neq j$. This is because (which I assume) $\{\,\tilde{u}^i\,\}$ and $\{\,u_j\,\}$ are dual bases of $V^*$ resp. $V$. All permutations other than the one given by $I$ vanish, esp. all odd ones.

Thanks fresh_42

Again ... most helpful ...

Peter