cbarker1
Gold Member
MHB
- 345
- 23
Dear Everybody,
How to get started for this problem?
An Earth satellite has its apogee at 2,400 km above the surface of Earth and perigee at 750 km above the surface of Earth. At apogee its speed is 6,800 m/s. What is its speed at perigee (in m/s)? Earth's radius is 6,370 km (see the figure below, which is not drawn to scale)
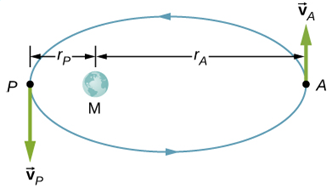
Thanks,
Cbarker1
How to get started for this problem?
An Earth satellite has its apogee at 2,400 km above the surface of Earth and perigee at 750 km above the surface of Earth. At apogee its speed is 6,800 m/s. What is its speed at perigee (in m/s)? Earth's radius is 6,370 km (see the figure below, which is not drawn to scale)

Thanks,
Cbarker1