Speed of the rod as it leaves the rails?

[nawand]

Homework Statement

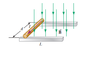
A rod of mass 0.720 kg and radius 6.00 cm rests on two parallel rails fig.1 that are the d=12.0 cm apart and L=45.0 cm long. The rod carries a current of I=48.0 A in the direction shown and rolls along the rails without sleeping. A uniform magnetic field of magnitude 0240 T is directed perpendicular to the rod and the rails. If it starts from rest, what is the speed of the rod as it leaves the rails?

Homework Equations

0+0+F_b *L*cos θ = (mv²)/2 +(Iω²)/2

The Attempt at a Solution

The rod gains energy from the rest, so begin kinetic energy and rotational energy are zero. The only source of energy rod gains is magnetic filed.
I = (mr²)/2
K=(mv²)/2
w=v/r
That is right side of equations becomes:
(mv²)/2 + 1/2 (mv²)+1/2(1/2 mr²) * (v²/r²)

F_b * L = 3/4 mv²
Where
F_b = I * d * B
etc
v=1.07 m/s

Because the force move the rod parallel to the rails along x axis, the dot product will be:
E=F_b * L * cos θ = F_b*L*1=F_bL
The question is how do we get the value of energy exerts magnetic field on the rod?
That is force time Length of rails (F_b times L)?

For the electric field is E = qF_e

 

[mfb]

(mv²)/2 + 1/2 (mv²)+1/2(1/2 mr2) * (v2/r2)

It looks like you are adding the kinetic energy twice here (highlighted in bold).
The line afterwards is right again.

The question is how do we get the value of energy exerts magnetic field on the rod?
That is force time Length of rails (F_b times L)?

Sure.

I don't see an electric field.

Slipping, not sleeping, by the way.

 

[nawand]

Great!.

Indeed I have added it twice mv²/2 (This is my type fault).

• I was wondering about the energy was added in the left side Fb times L and which is likely the energy contribution of magnetic field.
• "Sleeping" = "Slipping"

Thanks a lot!