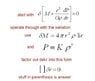Spherical star in a hydrostatic equilibrium

[ted1986]

Hello again,

I've got a question about a star in a hydrostatic equilibrium.
How do I derive an equation of motion for a pertubation in the full momentum equation? I'm attaching my solution (my_solution.jpg) , but I'm not quite sure about it.

The full exercise is attached as astro_problem.jpg.

Thank you.

 

[Ken G]

It's not that simple, the meaning of "d" and "delta" are different. The meaning of "d" is "a change as you change location", but the meaning of "delta" is "perturbed from the original equation." So before you substitute and delta expressions, you first have to find the momentum equation that applies to the delta variables. When you're all done, you'll still have d/dr kinds of things, but they will apply to the delta variables, not the P and rho by themselves.

 

[Helios]

I think I did this once. I even thought it was my idea. Don't use their hints, see attachment. The "del" works like del f = f' del r.

 

[ted1986]

I think I did this once. I even thought it was my idea. Don't use their hints, see attachment. The "del" works like del f = f' del r.

OK, I tried to solve the exercise as you said (P=K*rho^\gamma), but the equaion I've got seems to be to complicated... (my derivation is attached - star_my_sol2.jpg)

Perhaps the derivation needed to solve it is less complicated?

Thank you.

 

[Helios]

Sorry, but that's way off because the way you related density and mass. Your equation would only work for mean density, were M the total mass. Their relationship is instead differential.
The knack here is to apply the variation ( perturb ) and then factor out ( linearize ) the del-r out. Since the variation is arbitrary, the parenthetical stuff must equal zero ( the derived equation ).
I don't get the hints they gave.

 

[ted1986]

Thank you for your efforts :)