Suyash Singh
- 168
- 1
Homework Statement
Homework Equations
only basic school level physics will be needed in this question.
The Attempt at a Solution
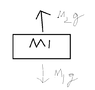
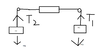
The mass m1 pulls spring from first side and m2 pulls spring from the other side therefore reading should be m1-m2.
But my answer is wrong.
I can't understand what to do.