Static Equilibrium: Finding Coefficient of Friction with Torque Analysis

[SnakeDoc]

Homework Statement

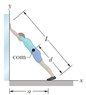
In the figure, a climber leans out against a vertical ice wall that has negligible friction. Distance a is 0.905 m and distance L is 2.15 m. His center of mass is distance d = 0.91 m from the feet-ground contact point. If he is on the verge of sliding, what is the coefficient of static friction between feet and ground?

Homework Equations

x: 0= W-ƒ
y: 0= N+mg
Torque
T=L x F
0= N(A)-(1.95)ƒ-(.52195)mg
ƒ=μN

The Attempt at a Solution

I drew a FBD and came up with
x: 0= W-ƒ
y: 0= N+mg
putting them in a state of equilibrium.

Find than
then I did the torques and

T: 0 = Nτ-ƒτ-mgτ

Unsure how to proceed I used the WileyPlus' go tutorial feature it asked me for what it called the moment arms of the Normal force, Force due to gravity, and frictional force after a few guesses because I was unsure what it was asking for it gave all three values but I would like to know what it was asking for how =to find them. The values were as follows
moment arm for Normal force: .905
moment arm for Force due to Gravity: .52195
moment arm for Frictional Force: 1.95
I understand that they become the L value of each torque but I don't understand how they found each.

T: 0= N(.905)-ƒ(1.95)-mg(.52195) since N=MG and ƒ=mg substitute
T: 0= mg(.905)-μmg(1.95)-mg(.52195)<<mg's cancel
T: 0=(.905)-μ(1.95)-(.5195) <<simplify
T: μ=.196

 

[DTM]

You need to find the perpendicular distance from each force to the point you are taking the moment about. You can draw a "line of action", extending each force vector in both directions. Then draw in the perpendicular line between the force line of action and the point you are taking the moment about. Then you need to use your trigonometry to find those moment arms.