SUMMARY
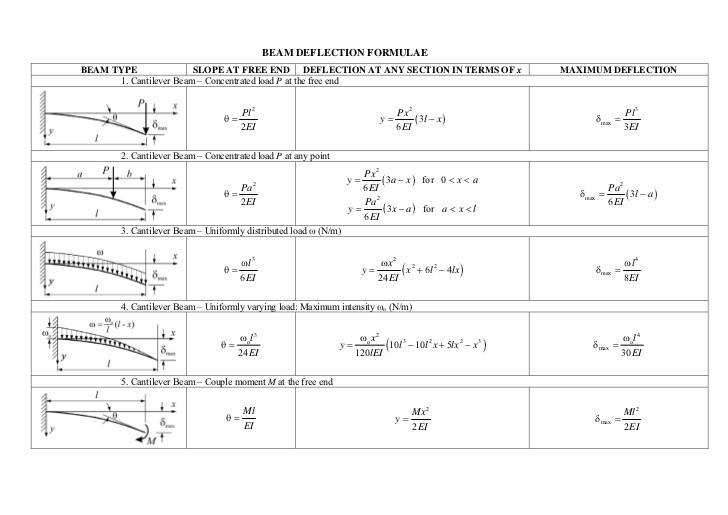
The discussion centers on the application of deflection equations in statically indeterminate structures, specifically when to use maximum deflection equations versus simple deflection equations. It is established that one should utilize the most general deflection formula applicable to the beam and loading arrangement. In cases such as propped cantilevers, the maximum deflection formula can be derived from the general deflection equation by substituting the length of the cantilever. This approach ensures accurate calculations for reactions in statically indeterminate problems.
PREREQUISITES
- Understanding of statically indeterminate structures
- Familiarity with deflection equations in structural engineering
- Knowledge of cantilever beam mechanics
- Ability to evaluate loading arrangements on beams
NEXT STEPS
- Study the general deflection equations for various beam types
- Learn about propped cantilever beam analysis
- Research specific maximum deflection formulas for different loading conditions
- Practice solving statically indeterminate problems using deflection equations
USEFUL FOR
Structural engineers, civil engineering students, and professionals involved in the analysis and design of beams and load-bearing structures will benefit from this discussion.