SUMMARY
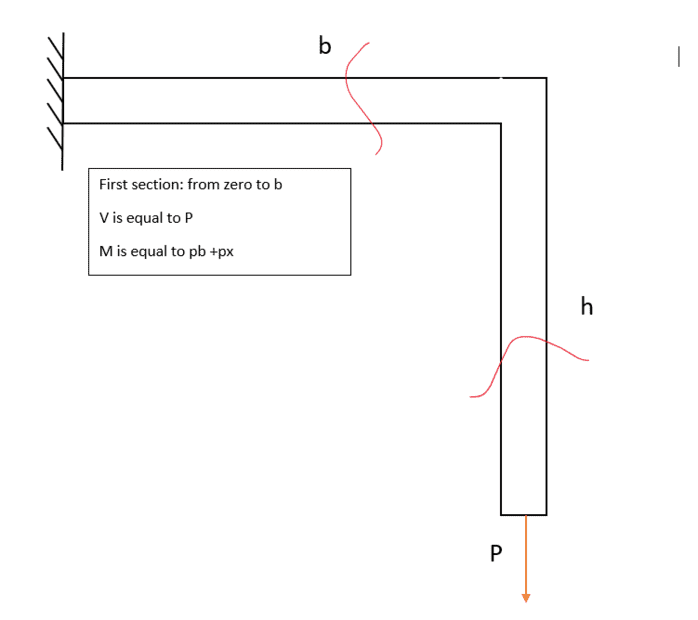
This discussion focuses on analyzing beam forces and moments in statics problems, specifically addressing the confusion between "moment" and "momentum." Participants clarify that in statics, momentum is not involved, and the correct approach involves balancing forces and moments. The moment in the horizontal section is defined as P(b-x), and it is emphasized that starting the analysis from the end of the beam simplifies the process. A constant momentum of zero is established at the h section, reinforcing the importance of understanding the distinctions between these concepts.
PREREQUISITES
- Understanding of statics principles
- Familiarity with beam analysis techniques
- Knowledge of force and moment balance
- Ability to differentiate between moment and momentum
NEXT STEPS
- Study beam analysis methods in statics
- Learn about force and moment equilibrium in structural engineering
- Explore cantilever beam theory and applications
- Investigate common mistakes in statics problems, particularly regarding terminology
USEFUL FOR
Students and professionals in engineering, particularly those specializing in structural analysis, mechanics, and statics. This discussion is beneficial for anyone looking to deepen their understanding of beam forces and moments.