Steinhart Temperature vs. Actual Temperature from thermistor resistance

[HyperSniper]

I'm pretty confused on what the difference between what the temperature reading is from a thermistor vs. the Steinhart Temperature.

Basically I know that the "Steinhart–Hart equation" is given as:

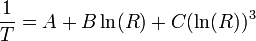
However, the http://www.vishay.com/docs/29049/23816403.pdf" for the thermistor I am using gives it's temperature value as a function of resistance as:

[PLAIN]http://img863.imageshack.us/img863/2293/unled1bo.png

Where R_ref is the resistance at a reference temperature of 25 degrees C.

When I plug in my values for the resistance and the given values for A, B, and C into the "Steinhart–Hart equation" the values are far, far, too low to be correct. However the equation from the datasheet works just fine.

So what it kind of looks like to me is that to get the "Steinhart–Hart equation" to work I would have to get the coefficients from known temperatures, is that correct or am I just completely off?

 

[jsgruszynski]

Basically are saying exactly the same thing.

There's an algebraic substitution of R = R/Rref, they've taken the reciprocal of both sides and there's a change of variable name. All are basically "no difference" changes.

The only add bit is they've added a square term (basically making it a real power series) in the real device. This makes sense because the Steinhart–Hart equation is an ideal theoretical equation which likely is not be representative of practical devices.

Adding a square term is 100% logical in this case because you generally get greater accuracy with higher order terms and the added the square term probably should have been there anyway if you are using a power series approximation like Steinhart–Hart equation to be completely general.

The extra square term simply helps the curve fit of real measured device performance because real devices are seldom ideal like the Steinhart–Hart equation.

What I would do is use the datasheet formula for anything involving design or characterization using that device. I would only use the Steinhart–Hart equation as a "challenge" fit equation - if it fits, great, use it instead, otherwise, dump it.

You can work some algebra+calculus to predict what corners of operation will fit the Steinhart–Hart equation and the datasheet formula similarly and which will not. That would tell you the same kind of "fitness" answer.

The extra terms in the datasheet equation means it is impossible to fit the Steinhart–Hart equation to all regions of the datasheet equation, and thus likely the device itself.

Extra terms == extra information. Going from datasheet to Steinhart–Hart equation is throwing away characterization and measurement information. The fit and region accuracy are a measure of how much information is lost. In general, you never want to consciously throw out measurement information until you must/can - it's an entropic one-way transformation.

 

[HyperSniper]

Ah, thanks so much! I was too confused at the time to articulate my question properly which was basically: "Why is this different from this?" Thanks again!