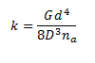Stiffness Equation for Spring Dimensions: How is it Derived?

[ajd-brown]

Equation attached.

For those who can't see the image here it is in text form, k=(Gd^4)/(8D^3 n )

It is the equation for the stiffness of a spring in terms of its dimensions:

G - shear constant
d - wire diameter
D - coil average diameter
n - number of active coils (total coils -2 as the top and bottom coils are not considered active)

I would like to know how to derive this equation as it is a big chunk of my project,

I am doing this as part of a university project, and your derivation will be duly noted/referenced.

Thanks in advance!

Anthony

 

[Studiot]

Since you are at university, why can you not look this up for yourself in a mechanics of materials text in the library?

For instance page 82 - 83 of

Singer

Strength of Materials

or

Hearn

Mechanics of Materials p299 to 301

 

[ajd-brown]

I'll do that now, thank you for the book!

 

[tadchem]

This may be helpful:
Deriving the Shear Modulus S From the Spring Constant k
http://faraday.physics.utoronto.ca/PHY182S/WilberforceRefShearSpringConstant.pdf
As a math student I learned that sometimes the answer is most easily found by working backwards.

 

[ajd-brown]

yeah! i found that post very helpful for understanding the concept, jheez, i love this stuff, i wish i could have the time in the day to learn it all, along with everything else i want to do :( anyway! thank you very much! best first post ever i think!