- #1
cantgetaname
- 41
- 0
I'm trying to understand how the Navier-Stokes equations are derived and having trouble understanding how the strain rates are related to shear stresses in three dimensions, what a lot of texts refer to as the 'Stokes relations'.
http://soliton.ae.gatech.edu/labs/windtunl/classes/hispd/hispd06/ns_eqns.html
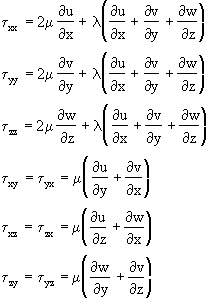
It's no longer the simple stress=viscosity*velocity gradient of the 1d case, but more complicated than that and none of the books I could get my hands on or the internet could show me how these relations are derived. They are just mentioned there as if they are obvious but I can't see how.
And what does the normal components in viscous shear stress tensor (τxx, τyy, τzz) even mean? How can you have viscous shear stress normal to a surface.
http://soliton.ae.gatech.edu/labs/windtunl/classes/hispd/hispd06/ns_eqns.html
It's no longer the simple stress=viscosity*velocity gradient of the 1d case, but more complicated than that and none of the books I could get my hands on or the internet could show me how these relations are derived. They are just mentioned there as if they are obvious but I can't see how.
And what does the normal components in viscous shear stress tensor (τxx, τyy, τzz) even mean? How can you have viscous shear stress normal to a surface.