Javier Lopez
- 74
- 3
Hello, I need the stopping power for a proton ion gun through Boron-11 sheet 1mm thick.
I have the following table obtained from here:
https://www-nds.iaea.org/stopping/stopping_hydr.html
Where the unit is in 1-15*eV*cm2/atom:
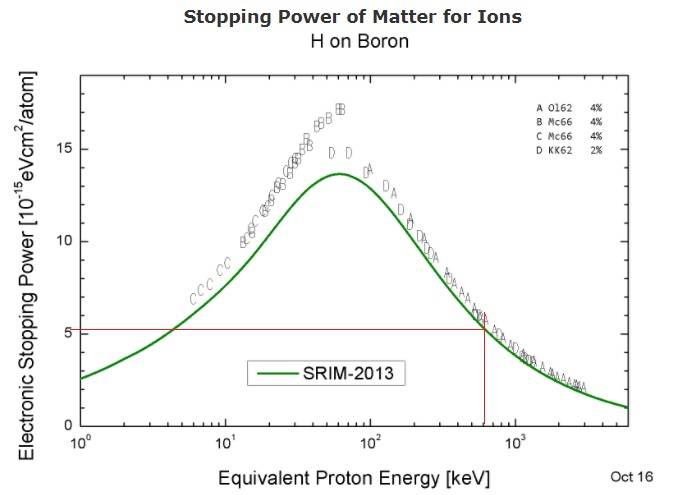
Then I calculated for 600keV protons at table 5.1eV*cm2/atom.
I calculated for Boron which density is 2080kg/m3 and atomic number 11 a density of 1.139atoms/m3
So the stopping power should be:
5.1*1e-6 (MeV/eV) * 1e-4 (cm2/m2) /1.1389 *.001=58e6 MeV
That is too much (at least 1e6 times), what I did wrong?
I have the following table obtained from here:
https://www-nds.iaea.org/stopping/stopping_hydr.html
Where the unit is in 1-15*eV*cm2/atom:
Then I calculated for 600keV protons at table 5.1eV*cm2/atom.
I calculated for Boron which density is 2080kg/m3 and atomic number 11 a density of 1.139atoms/m3
So the stopping power should be:
5.1*1e-6 (MeV/eV) * 1e-4 (cm2/m2) /1.1389 *.001=58e6 MeV
That is too much (at least 1e6 times), what I did wrong?
Attachments
Last edited by a moderator:
