Strange result from taking logs of logs in experimental data

[Tcbovb]

I have some experimental data (not hypothetically, this is real data), which has a downward sloping shape.

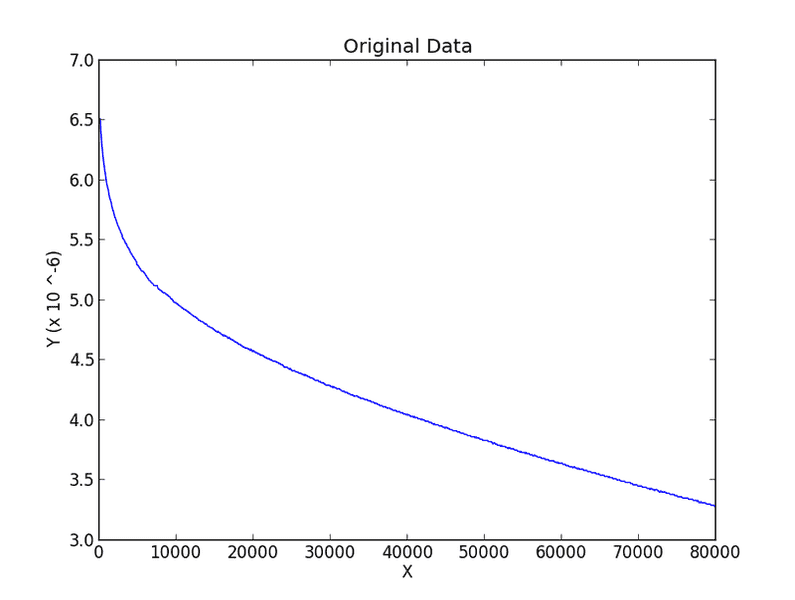
A sharp decrease initially, before settling to what looks almost like a downward linear slope. To investigate further, I decided to take the base 10 log of the y-axis data. The plot looked almost the same:

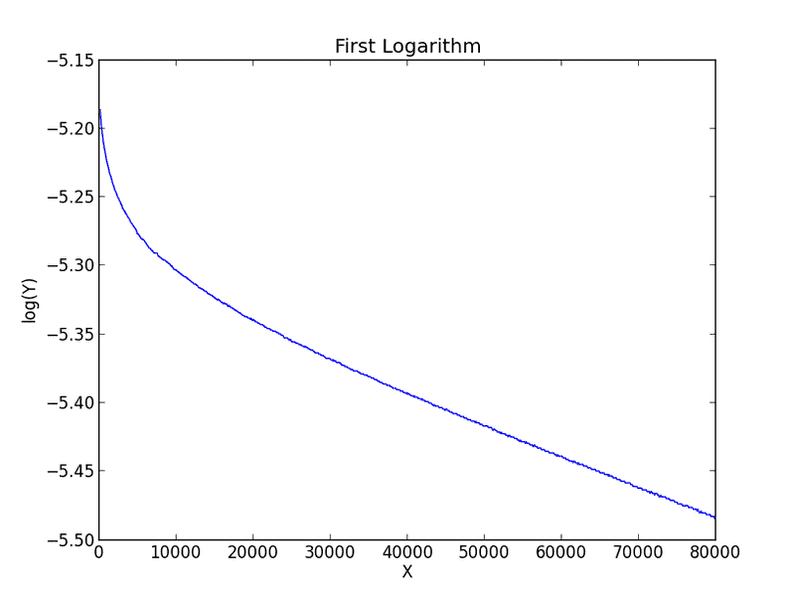
At first I though this was a mistake, but I checked over the values and the code I used to generate this and it seems fine. If the right hand part is a slowly decaying exponential, this will appear approximately linear for both linear and logarithmic axes, so maybe that is the explanation. I tried to see if I could get the curves to overlap by scaling and shifting all the values equally, but that isn't quite possible (as one would expect). However these curves do seem to be "similar" in a sense.

So I then took the log of the absolute values of the logarithmic data. Doing this over and over again produced the same familiar curve, though sometimes it was mirrored, becoming an increasing function. After 10 logs to the original data [log(log(log ... log(Y)))], this curve finally breaks down, in part because the data before (9 logs) passes through Y = 0.

What I am wondering is what is the name of a function in which when you take the log of it, the resulting function also appears to have the same shape? What functions satisfy this condition and what is the name of such similarity?

Perhaps this is just the result of something straightforward that I haven't considered yet. At the moment it just seems so weird.

Attached are a few more plots. Data points occur every 100 in the X axis. Some consecutive data points have the same Y values, hence the square corners that seem to appear in the plots.

Hopefully this is the right forum for this, I'm not really sure where "unexpected results from data analysis leading to mathematical curiosity" fits in.

Tcb

 

[The_Duck]

What I am wondering is what is the name of a function in which when you take the log of it, the resulting function also appears to have the same shape?

Any function whose range isn't too large will have this property, at least approximately. As an example, consider the function f(x) = 1 + g(x) where g(x) is some other function, and |g(x)| is always much smaller than 1. Then

$\ln(f(x)) = \ln(1 + g(x)) = g(x) - g(x)^2/2 + g(x)^3/3 - ...$

where I used the Taylor series expansion of ln(1+x) on the right-hand side. If
|g(x)| is much smaller than 1, then all the extra terms on the far right are very small compared to g(x), so $\ln(f(x)) \approx g(x)$.

But f(x) and g(x) have the same shape; f(x) is just shifted up by 1.

In fact, this argument is not specific to the logarithm function. You can convince yourself that essentially the same steps will work if you replace the logarithm with essentially any other function.

 

[Tcbovb]

Sure, that makes sense, but I am wondering if a Taylor series approximation fully explain what is going on here.

The data is certainly shifted, but it's not just shifted. The overall scaling of the function is different as well. Perhaps it's also due in part from the way the plots chose the y-axis scale so that the log taken plot looks more like the original data.

 

[Chestermiller]

Try the sum of a linear decay and an exponential decay. Something like A - x/B+C exp(-x/D). A will be about 4.9 and C will be about 1.6. B will be about 50000, and D will be about 7000.

Chet

 

[JJacquelin]

I have to correct my first answer. In fact, there was a mismatch between the data files to be ploted in the drawing software. The fitting is not so good than shown on the preceeding figure. It was too good to be true. I am sorry for the mistake. Now, the corrected answer :
The fit obtained with the function y = a + b x^c leads to a mean squares deviation = 0.0354
On the attached figure, the computed curve (in red) is close to the original curve (in blue).
First, the original curve has been scanned in order to pick about 300 points with a convenient software.
Second, the values of the parameters a, b, c were computed thanks to the very simple method described pp.16-17 in the paper "Régressions et équations intégrales" (written in French, but the formulas to be applied are understandable in any language). Published on Scribd :
http://www.scribd.com/JJacquelin/documents
The method of regression is straigthforward (process not itterative, no need for a guessed initial value).
Of course you could as well use a more common method for non-linear regression, but you will be prompted to give an initial guess for the parameter c.

 

[JJacquelin]

An almost as good fitting is obtained with y = a + b*x + 1/(c*x + d) : Figure in attachment
The mean squares deviation is slightly higher and the déviations are more important in the range of small values of x. But the déviations are clearly lower in the range of large values of x.

 

[JJacquelin]

An even better fit is obtained with y = a₀+ a₁x + b x^c
Mean squares deviation = 0.0107
The computation of the values of parametres was done with the method of transformation of the non-linear equation to a linear equation thanks to a convenient integral equation (paper already referenced above).