vktsn0303
- 30
- 0
I was reading about strain rate tensors and other kinematic properties of fluids that can be obtained if we know the velocity field V = (u, v, w). It got me wondering if I can sketch streamlines if I have the strain rate tensor with me to start with. Let's say I have the strain rate tensor:
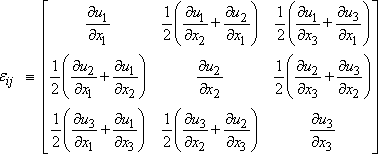
Would it now be possible to sketch the flow field and determine the flow direction from this? If yes, how?
Also, in 2D potential flows streamlines are perpendicular to potential lines. Does this mean in 3D the set of streamlines will be a plane with a line perpendicular to it? And can this also be explained with just the help of the strain rate tensor above by solving an eigenvalue problem?
Would it now be possible to sketch the flow field and determine the flow direction from this? If yes, how?
Also, in 2D potential flows streamlines are perpendicular to potential lines. Does this mean in 3D the set of streamlines will be a plane with a line perpendicular to it? And can this also be explained with just the help of the strain rate tensor above by solving an eigenvalue problem?