Stress tensor rotation/shear stress

[sthoriginal]

Hi. I have a huge problem and without solving it I can't move forward. I will appreciate any help.

Having the stress tensor S:

163.666557052527 -63.0272557558942 0.000000000000000E+000
-63.0272557558942 70.3802282767392 0.000000000000000E+000
0.00000000000000 0.00000000000000 0.000000000000000E+000

σ11 - North, σ22 - East, σ33 - Down

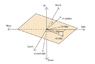
I have to calculate the normal stress and shear stress in slip direction for this focal mechanism

α - strike = 315°, β - dip = 73°, and λ - rake(slip) = 55°.

I think I know how to calculate the normal stress but I have no idea how to compute the shear stress in slip direction (55°)

Please help!

M.

 

[Chestermiller]

Welcome to Physics Forums

You need to determine the components of a unit normal to your plane. To get the stress vector on the plane, you then dot the stress tensor with the unit normal. The normal component of the stress vector is then determined by dotting the stress vector with the unit normal. The shear component of the stress vector is whatever is left over. So, if $\vec{\sigma}$ is the stress tensor, $\vec{n}$ is the unit normal, and $\vec{s}$ is the stress vector on the plane, then
$$\vec{s}=\vec{\sigma}\centerdot \vec{n}$$
Normal component of stress vector = $\vec{s}\centerdot \vec{n}=\vec{n}\centerdot \vec{\sigma}\centerdot \vec{n}$

Shear stress on plane = $\vec{s}-(\vec{s}\centerdot \vec{n})\vec{n}$

 

[sthoriginal]

Thanks very much for your reply. I really appreciate that.
I understand everything what you've just put there. the only one thing I can't get is when should I use the rake angle to calculate stress in dip direction?

I know I should use these direction cosines for the normal to the plane :
n=
| cos(strike)*sin(dip) |
| -sin(strike)*sin(dip) |
| cos(dip) |

The using my initial vector:

163.666557052527 -63.0272557558942 0.000000000000000E+000
-63.0272557558942 70.3802282767392 0.000000000000000E+000
0.00000000000000 0.00000000000000 0.000000000000000E+000

and n I can calculate the traction vector on that plane, and from that the normal to the plane (following your equation). However, using your shear stress equation, I will only get the shear stress in dip direction. Could you please help me resolve it in the slip direction? Any help will be hugely appreciated>

Thanks in advance

 

[Chestermiller]

Sorry. I understand that the strike and dip identify the specific plane upon which you are determining the traction vector. But, I'm not familiar with the term rake or slip. I'm guessing you are trying to resolve the shear component of the traction vector into its component in a particular direction within the plane. Maybe you can help me by defining the slip/rake direction.

Chet

 

[sthoriginal]

Hi Chat,

Thanks for your reply.

The slip is the direction in which the dislocation moves, usually measured from the direction of the strike (I attached two images). And what I need to do is to resolved the traction vector into its shear component in this particular shear direction within the plane.

Thanks a lot for your help

 

[Chestermiller]

Hi Chat,

Thanks for your reply.

The slip is the direction in which the dislocation moves, usually measured from the direction of the strike (I attached two images). And what I need to do is to resolved the traction vector into its shear component in this particular shear direction within the plane.

Thanks a lot for your help

I'm not sure. If I had to guess, what I would do would be to dot the shear stress vector with a unit vector in the slip direction.