Stretched spring attached to the center of a pure rolling disk

[Thermofox]

Homework Statement

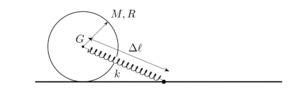
A homogeneous disk, with mass $M = 1 kg$ and radius $R = 0.2 m$, is placed on a rough plane on which it is able to move with pure rolling motion. The center $G$ of the disk is connected to an ideal spring, with negligible rest length and elastic constant $k = 10 N/m$, fixed to the plane as shown in the figure. At the initial instant, the spring is stretched by $Δl = 0.5 m$ and the disk is at rest.

Relevant Equations

$F_s= k \Delta l$
$\Sigma F = ma$

I need to determine:
1) The initial acceleration of the disk
2) the speed of the disk when the spring reaches minimum displacement

For point one I think I should use the free body diagram and then $\Sigma F = ma$, I'm taking as positive the right and the upward directions and the counter clockwise direction:
$\begin{cases} \Sigma F_x = ma \\ \Sigma F_y= 0 \\ \Sigma \tau = I \alpha \end {cases}$

$\begin{cases} F_{s,x} ?-? f = ma ; \text {I don't understand the supposed direction of the friction force, "f".}\\ N - F_{s,y} = 0 \\ \tau_f = I \alpha \end {cases}$
Is $f$ opposed to $F_{s,x}$, thus it is directed towards the left, because the disk is not moving. Or is it directed towards the right, since it opposes to the movement of the point of contact between the plane and the disk?
The second equation is not useful to the resolution of the problem then:

$\begin{cases} F_{s,x} ?-? f = ma \\ ?-?fR= I \alpha \end {cases}$
Now I have another problem since I don't know how to define $F_{s,x}$. I can only determine $F_s$, but how can I determine the x-component?

Lastly for point 2, the spring reaches the minimum stretch when the spring is perpendicular to the plane and therefore when it has the same length of the radius, $R$.

 

[haruspex]

I don't understand the supposed direction of the friction force, "f".

You don't have to predict this. Just take it as positive right, per your convention. The sign that comes out of the algebra will tell you.

$N - F_{s,y} = 0$

Gravity?

Now I have another problem since I don't know how to define $F_{s,x}$. I can only determine $F_s$, but how can I determine the x-component?

Trigonometry. You know two sides of a right-angled triangle.

Lastly for point 2, the spring reaches the minimum stretch when the spring is perpendicular to the plane and therefore when it has the same length of the radius, $R$.

Right.

 

[erobz]

Lastly for point 2, the spring reaches the minimum stretch when the spring is perpendicular to the plane and therefore when it has the same length of the radius, $R$.

The center $G$ of the disk is connected to an ideal spring, with negligible rest length and elastic constant $k = 10 N/m$,

My interpretation is that is has no (zero) initial length in the unstretched state? So if $G$ were over the anchor point, it has zero length. Just asking if anyone else believes that is plausible interpretation or not.

EDIT: I still don't understand the significance of the wording there, but I see that having zero initial length is a physical impossibility now! As you were...

 

[Lnewqban]

As Fx decreases from maximum (initial) to minimum stretching or displacement, it seems that this approach may be needed for determining 2):
http://hyperphysics.phy-astr.gsu.edu/hbase/acons.html#c3

 

[haruspex]

As Fx decreases from maximum (initial) to minimum stretching or displacement, it seems that this approach may be needed for determining 2):
http://hyperphysics.phy-astr.gsu.edu/hbase/acons.html#c3

I'm not sure what the author at that link intends by "time-dependent acceleration". If it just means not constant, the question becomes whether it is a known function of time or of something else, like position or velocity.
In the present case, it is a known function of position. That often means it is easier to solve using conservation laws.

 

[Lnewqban]

In the present case, it is a known function of position. That often means it is easier to solve using conservation laws.

Then, would it be correct to think that the liberated elastic potential energy will become rotational plus linear kinetic energies?

 

[haruspex]

Then, would it be correct to think that the liberated elastic potential energy will become rotational plus linear kinetic energies?

Yes.

 

[Thermofox]

I'm sorry I didn't answer, but I suddenly got sick and had no strengths to write.

Gravity?

Yes, I forgot that $\Rightarrow N - F_{s,y} - Mg = 0$

Trigonometry. You know two sides of a right-angled triangle.

I saw that, but got confused because what I found was just a length. Now I realize that I can find $F_{s,x}$ by multiplying the length I found by the elastic constant, since $F_{s,x}$ it's still an elastic force.

You don't have to predict this. Just take it as positive right, per your convention. The sign that comes out of the algebra will tell you.

I wasn't sure wether friction pointed towards the right or the left, as shown in the picture. But I think it is safe to assume that, in this case, friction always points to the right, since the pure rolling motion starts immediately. Friction would point to the left only if the disk was sliding or if it would be rotating counter clockwise.

Right.

Then I can say that:
$E_{\text{initial}} = E_{\text{final}} \Rightarrow \frac 1 2 k \Delta l_{\text{initial}}^2 = \frac 1 2 m v^2 + \frac 1 2 I_G \omega^2 + \frac 1 2 k \Delta l_{\text{final}}^2$. I know that $\Delta l_i= 0.5$, $\Delta l_f= 0.2$ and that $\omega= vR$. Therefore: $$k(\Delta l^2_i - \Delta l^2_f )= v^2( m + I_G R^2) \Rightarrow v= \sqrt{\frac {k(\Delta l^2_i - \Delta l^2_f )} {( m + I_G R^2)}}$$

 

[Thermofox]

My interpretation is that is has no (zero) initial length in the unstretched state? So if $G$ were over the anchor point, it has zero length. Just asking if anyone else believes that is plausible interpretation or not.

EDIT: I still don't understand the significance of the wording there, but I see that having zero initial length is a physical impossibility now! As you were...

Honestly, neither do I. I think the problem wants to exaggerate the fact that in this case the spring never "un-streches"? I don't know.

 

[haruspex]

Therefore: $$k(\Delta l^2_i - \Delta l^2_f )= v^2( m + I_G R^2) \Rightarrow v= \sqrt{\frac {k(\Delta l^2_i - \Delta l^2_f )} {( m + I_G R^2)}}$$

Right, and you can figure out $\Delta l_i, \Delta l_f$ and $I_G$, yes?

It is not unusual for a zero relaxed length to be specified, though unrealistic, to simplify the algebra.

 

[Thermofox]

Right, and you can figure out $\Delta l_i, \Delta l_f$ and $I_G$, yes?

$\Delta l_i$ is given, $\Delta l_f$ is the minimum displacement of the spring which is $R= 0.2m$ and $I_G= \frac 1 2 M R^2$ since it is a disk. I know everything so I can finish the problem. Thank you!

 

[haruspex]

$I_G= \frac 1 2 M R^2$ since it is a disk.

A homogeneous disk, in fact.