Fat Ryan
- 48
- 0
Im so lost in Statics :( :( HELP!
first of all i need to say that i do not go to a school that is known for its sciences. this of course means that we have crappy science teachers because our budget is very low. my teacher is horrible at explaining the material and whenever i ask him a question he does not explain the solution even remotely clear. I've tried the book but its pretty useless too (2 examples per 30-40 problems). the tutors on campus can pretty much only help with general physics so i guess this is my last hope.
we are working on truss assemblys and i can't understand how this whole force moment thing works. the solutions that i calculate don't make sense when i try to visualize the situation.
here is one of my homework problems that i have been stuck on for a while now:
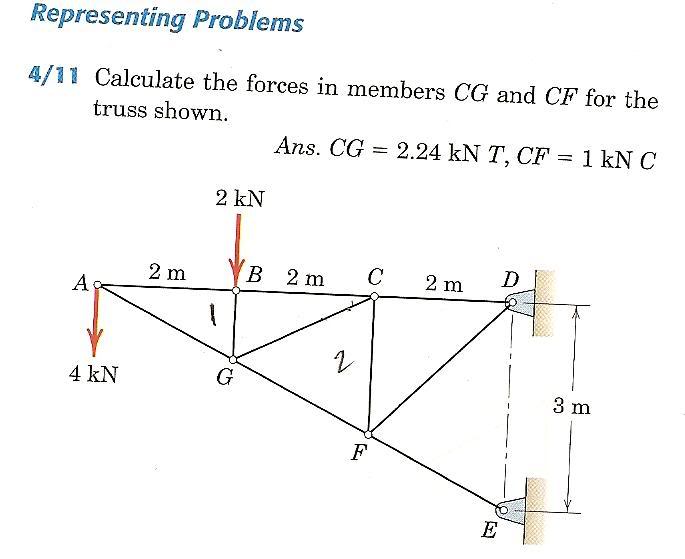
where do i begin the calculations?
when calculating the Fy forces should i include point E or just use one at a time (D & E)?
do i need to take the moment about some point? (i tried C and D, but both didnt seem right)
can someone PLEASE give me a clear and precise explanation on how to solve problems like this?
this is all i have so far and i doubt its correct:
but this just doesn't make sense for D...
first of all i need to say that i do not go to a school that is known for its sciences. this of course means that we have crappy science teachers because our budget is very low. my teacher is horrible at explaining the material and whenever i ask him a question he does not explain the solution even remotely clear. I've tried the book but its pretty useless too (2 examples per 30-40 problems). the tutors on campus can pretty much only help with general physics so i guess this is my last hope.
Homework Statement
we are working on truss assemblys and i can't understand how this whole force moment thing works. the solutions that i calculate don't make sense when i try to visualize the situation.
here is one of my homework problems that i have been stuck on for a while now:
Homework Equations
where do i begin the calculations?
when calculating the Fy forces should i include point E or just use one at a time (D & E)?
do i need to take the moment about some point? (i tried C and D, but both didnt seem right)
can someone PLEASE give me a clear and precise explanation on how to solve problems like this?
The Attempt at a Solution
this is all i have so far and i doubt its correct:
Code:
SUM Fx=0...Dx=0
SUM Md=0...4kN(6m) + 2kN(4m) - A(6m)=0
A= 5.333kN
SUM Fy=0...5.333kN - 4kN - 2kN + D = 0
D= 0.667kNbut this just doesn't make sense for D...