Goldenwind
- 145
- 0
[SOLVED] Summation Notation - Variable in the exponent
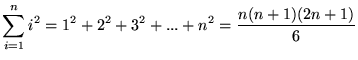
This is an example formula.
How do I solve a summation if something is in the form of Sum(c^i), where c is some constant?
Homework Statement
This is an example formula.
How do I solve a summation if something is in the form of Sum(c^i), where c is some constant?