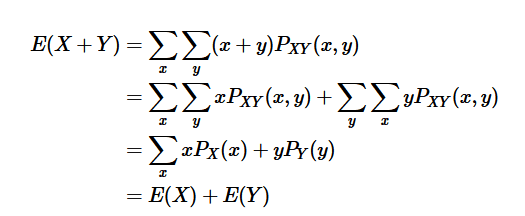Sum of the Expected Values of Two Discrete Random Variables

[TheBigDig]

Homework Statement

Prove that E[aX+bY] = aE[X]+bE[Y]

Relevant Equations

$$E[X] = \sum_{x=0}^{\infty} x p(x)$$

Apologies if this isn't the right forum for this. In my stats homework we have to prove that the expected value of aX and bY is aE[X]+bE[Y] where X and Y are random variables and a and b are constants. I have come across this proof but I'm a little rusty with summations. How is the jump from the second line to the third line made?

 

[FactChecker]

The probability, $P_X(x)$, for X taking a fixed value, x, is the sum over all values of Y of $P_{XY}(x,y)$. So that is substituted in the third line. Likewise, the sum over all values of X of $P_{XY}(x,y)$ is replaced by $P_Y(y)$.

 

[etotheipi]

It's because$$\sum_y x P_{XY}(x,y) = x \sum_y P_{XY}(x,y) = xP_X(x)$$where the second equality follows from the law of total probability.

N.B. I think you're missing a $\sum$ before the $y P_Y(y)$

 

[Stephen Tashi]

How is the jump from the second line to the third line made?

Have you studied joint distributions and their associated "marginal distributions"?

As an example, suppose $P_{X,Y}$ is given by
$P_{X,Y}(1,1) = 0.4$
$P_{X,Y} (1,2) = 0.2$
$P_{X,Y} (2,1) = 0.3$
$P_{X,Y}(2,3) = 0.1$

The associated marginal distribution for $X$ is:
$P_X(1) = 0.6 = P_{X,Y}(1,1) + P_{X,Y}(1,2)$
$P_X(2) = 0.4$

The term $\sum_x \sum_y x P_{X,Y}(x,y)$ denotes:

$( (1) ( P_{X,Y}(1,1) + (1)P_{X,Y}(1,2) ) + ( (2) P_{X,Y}(2,1) + (2)P_{X,Y}(2,2))$
$= (1) P_X(1) + (2)P_X(x)$

In the next line, the term $\sum_x x P_X(x)$ also denotes
$(1) P_X(1) + (2)P_X(2)$

 

[TheBigDig]

Have you studied joint distributions and their associated "marginal distributions"?

As an example, suppose $P_{X,Y}$ is given by
$P_{X,Y}(1,1) = 0.4$
$P_{X,Y} (1,2) = 0.2$
$P_{X,Y} (2,1) = 0.3$
$P_{X,Y}(2,3) = 0.1$

The associated marginal distribution for $X$ is:
$P_X(1) = 0.6 = P_{X,Y}(1,1) + P_{X,Y}(1,2)$
$P_X(2) = 0.4$

The term $\sum_x \sum_y x P_{X,Y}(x,y)$ denotes:

$( (1) ( P_{X,Y}(1,1) + (1)P_{X,Y}(1,2) ) + ( (2) P_{X,Y}(2,1) + (2)P_{X,Y}(2,2))$
$= (1) P_X(1) + (2)P_X(x)$

In the next line, the term $\sum_x x P_X(x)$ also denotes
$(1) P_X(1) + (2)P_X(2)$

Okay yes, this definitely seems like something I need to read up on. Our instructor is a little handwavy at the moment saying we'll come across these concepts later but I'm one of those people who needs to understand each element.

It's because$$\sum_y x P_{XY}(x,y) = x \sum_y P_{XY}(x,y) = xP_X(x)$$where the second equality follows from the law of total probability.

N.B. I think you're missing a $\sum$ before the $y P_Y(y)$

Thank you as well. Yes I think it is missing that. I found it online and just copied and pasted the image.