theakdad
- 210
- 0
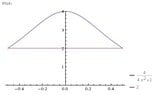
I have to calculate the surface area limited with two functions:
$$g(x)=2$$ and $$h(x)=\frac{4}{4x^2+1}$$
i was thinking first to calculate the points where this functions are intersecting by $$g(x)=h(x)$$ and to find corresponding $x$ for the intersection...and then to calculate definite integral somehow. Am i on the right path? Thank you for your help!
$$g(x)=2$$ and $$h(x)=\frac{4}{4x^2+1}$$
i was thinking first to calculate the points where this functions are intersecting by $$g(x)=h(x)$$ and to find corresponding $x$ for the intersection...and then to calculate definite integral somehow. Am i on the right path? Thank you for your help!