- #1
BnayaMeir
- 1
- 0
Thread moved from the technical forums to the schoolwork forums
Hi everyone!
I'm pretty new in this forum, I found the topics here very relevant to my physics course. And here is my question:
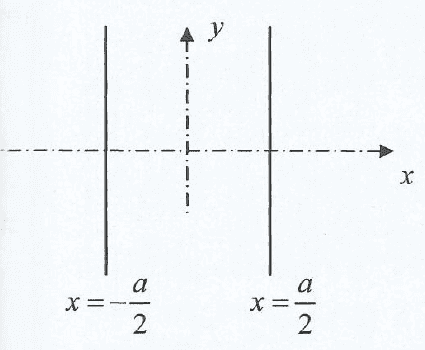
Given the following drawing, two infinite sheets (in y and z axis) of ideal conductive material. their thickness is infinitesimal (dx->0).
The electric field is defined:
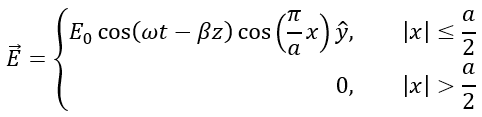
I have askes to find the surface charge and current density.
well.. I tried to apply the integral gauss law
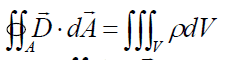but in 2 dimensions (didn't work).
I have also tries the derivative version of the law
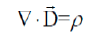which gave me zero. it looks right for me, since the electric field should be perpendicular to the surface. but the only electric field is parallel to the surfaces. Then where this field is come from?? I'm very confused..
I thought to find the current density after finding the charge density by the following equation in 2-D:
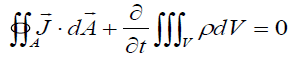
I hope you will be able to help me, thanks a lot!
I'm pretty new in this forum, I found the topics here very relevant to my physics course. And here is my question:
Given the following drawing, two infinite sheets (in y and z axis) of ideal conductive material. their thickness is infinitesimal (dx->0).
The electric field is defined:
I have askes to find the surface charge and current density.
well.. I tried to apply the integral gauss law
I have also tries the derivative version of the law
I thought to find the current density after finding the charge density by the following equation in 2-D:
I hope you will be able to help me, thanks a lot!