System of nonlinear differential equations

[havsula]

Hello
I have a system of differntial equations:
dx/ds = sin(p)
dy/ds=cos(p)
dp/ds = k
dk/ds = -1/EI(s)*(k*dEI/ds+f*sin(p))

x(0)=y(0)=p(0)=p(L)-pl = 0

These are nonlinear differential equations. I should use some sort of nonlinear finite difference. But I do struggle to setting up the finite difference system. I have found a lot of examples when we only have one differential equation for nonlinear finite difference.
But here I got 4 variables. Any suggestions?

 

[theodoros.mihos]

What $El(s)$ is?

 

[DEvens]

In a forum post, the most I will give is some pointers on where to look and what to look for.

You need to get yourself a text on numerical methods of solving differential equations. There are lots. It depends on the background you have, what language you are programming in, etc. For example, a popular one (if a bit rough-and-ready) is the Numerical Recipes series. C, Fortran, or Pascal, as you prefer. (I hear they now have C++ in one version.) The wiki pages are a good start but not enough.

http://en.wikipedia.org/wiki/Numerical_methods_for_ordinary_differential_equations
http://en.wikipedia.org/wiki/Numerical_partial_differential_equations

In your text that taught you how to do it with a single differential equation, you will have some kind of scheme that very roughly looks like this.

You divide the variable s into discrete steps, so you get s_n = 0,1, 2, 3, etc.
You use F(0) to calculate dF(0)/ds, and you use that to calculate F(1)
Then you have F(1) and you calculate dF(1)/ds, and you use that to calculate F(2).
And so on.

The naïve version of this is called Euler's method. It converges very slowly, meaning it gives poor accuracy for the amount of computation required.

Maybe your method is more clever and does some clever intermediate steps to get better convergence. So you should look up such things as Runge-Kutta.

For non-linear it is just the same. You only have a more complicated formula for dF/ds. And you have to be a bit more careful about convergence and stability. But it is still the same idea. You get F(0), you calculate dF(0)/ds, and you use that to calculate F(1). And so on.

For several equations coupled, you just do each variable in parallel. So you have
x(0)
y(0)
p(0)
k(0)

And you use them to work out
dx(0)/ds
dy(0)/ds
dp(0)/ds
dk(0)/ds

and then you use those to step to the next value of s. And so on.

I note that theodoros.mihos has asked what is El(s)? Its derivative shows up in the dk/ds equation. But neither El(s) nor k(s) have any boundary conditions. Are you sure you gave the full set of equations and boundary conditions? You have some interesting boundary conditions in that you have p(0) and p(L) specified. There are methods to deal with this. But check that you have the entire problem stated correctly first.

 

[SteamKing]

I think the OP's differential equations are using the flexural rigidity EI, rather than El(s), where E is Young's Modulus and I is the second moment of area of the cross section of the structural element of interest. This structural element may have stiffness properties which vary along the length coordinate, s.

In any event, as to solving a system of non-linear ODEs, any Runge-Kutta or similar method can be adapted to solve a system of linear or non-linear ODEs, if enough initial conditions are available.

It's not clear if this is some sort of elastic stability problem or what, since the OP has not shared what these equations model.

 

[havsula]

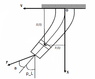
Sorry everybody. I wrote down the equations a little to fast. But here they are again, in proper latex:)

These equation is for large deflection of a flexible beam of length L.

I have got them from an article and trying to figure out how to solve them. In the article they state that they have used finite difference, but give no more information than that.s = position along the beam
x(s) = x position as a function of s
y(s) = y position as a function of s
p(s) = angle as a function of s
k(s) = kurvature as function of s
EI(s) = bending stiffness as a function of s

$\frac{\partial x}{\partial s}=cos(p)\quad x(0)=0$

$\frac{\partial y}{\partial s}=sin(p)\quad y(0)=0$

$\frac{\partial p}{\partial s}=k\quad\quad p(0)=0,p(L)=p_L$

$\frac{\partial k}{\partial s}=-\frac{1}{EI(s)}\left\{ k\frac{dEI}{ds}+Fsin(p_{L}+a-p\right\}$

I have been able to transforme these equations into a finite difference form by using central difference. I do know that they have used central idfference:
$\frac{\partial f}{\partial x} = \frac{f_{i+1}-f_{i-1} }{2h}$
The first differential equation then become:
$\frac{x_{i+1}-x_{i-1} }{2h} =cos(x_i)$

I do understand that I probably have a lot of reading to do before I can set up everything correct.
But my main questions is:

1.How can a know that I have enough boundary conditions. As you can see there is no boundary condition for curvature. There is also different number of boundary condition for the different equations. Do I not need at least two conditions for each differential equation?

2.I also struggle a little with how to handle that the differential at i=1 since I need i-1. A trick I have seen is to divide the beam into N+2 points and only use the interior points, but then I need boundary condition on both ends, which I do not have for all equations.

UPDATE
I have manage to set up the whole system for a beam divided into N+2 parts. Have onle set up the equations on the interior points 1 ot N. But I do not have enough boundary conditions to set up the system. For each differential equation f, I need both f_0 and f_(n+1) in order to get a complete system. But I cannot do that here since dx and dy only give med x_0 and y_0 and k do not give med k_0 or k_(n+1).

 

[SteamKing]

This article uploaded below discusses various approaches to solving the large deflection of beams. There are a variety of techniques which may be applied; finite differences and RK methods are but two.

The large deflection assumption for beam flexure means that things like superposition no longer apply. Each beam loading must be solved independently; you can't solve these problems as if the final result was the combination of several simpler problems.

 

[havsula]

This article uploaded below discusses various approaches to solving the large deflection of beams. There are a variety of techniques which may be applied; finite differences and RK methods are but two.

The large deflection assumption for beam flexure means that things like superposition no longer apply. Each beam loading must be solved independently; you can't solve these problems as if the final result was the combination of several simpler problems.

Thank you man. Now I have a lot of thing to read:)

 

[havsula]

Hello
I have finally found out what my main problem is:

I have manage to set up the whole system for a beam divided into N+2 parts. Have onle set up the equations on the interior points 1 ot N. But I do not have enough boundary conditions to set up the system. For each differential equation f, I need both f_0 and f_(n+1) in order to get a complete system. But I cannot do that here since dx and dy only give med x_0 and y_0 and k do not give med k_0 or k_(n+1).

Any suggestions?

 

[SteamKing]

Hello
I have finally found out what my main problem is:

I have manage to set up the whole system for a beam divided into N+2 parts. Have onle set up the equations on the interior points 1 ot N. But I do not have enough boundary conditions to set up the system. For each differential equation f, I need both f_0 and f_(n+1) in order to get a complete system. But I cannot do that here since dx and dy only give med x_0 and y_0 and k do not give med k_0 or k_(n+1).

Any suggestions?

This doesn't make any sense.

With a cantilever beam, you won't know what happens at point n+1 until the properties at all of the other nodal points 1-n are determined. If you had a beam which was simply supported at the ends, for example, then you would have a set of initial conditions at both ends which could be used.

If your beam is fixed at one end, it would seem logical to choose a solution method which requires using only the initial conditions at the fixed end and then solving the differential equations working along the length of the beam until you reach the free end.

Numerically, the choice of solution method will affect the accuracy of the solution and how quickly it converges, but otherwise, a solution is a solution, regardless of how it is obtained. Don't get too hung up on following another's work if it makes solving your own problem more difficult.

 

[havsula]

Hello
Okay I see that. It is only that if somebody says that a method works, I feel plain stupid (and maybe I am) if I cannot solve it in the same way.
But I still do not have a boundary condition for the fourth equations:

∂k/∂s=−1/EI(s){k*dEI/ds+F*sin(pL+a−p}

So still a little stucked.

 

[SteamKing]

Hello
Okay I see that. It is only that if somebody says that a method works, I feel plain stupid (and maybe I am) if I cannot solve it in the same way.
But I still do not have a boundary condition for the fourth equations:

∂k/∂s=−1/EI(s){k*dEI/ds+F*sin(pL+a−p}

So still a little stucked.

You can evaluate what dκ/ds is at the fixed end from the formula above. The variation in EI over the length of the beam is determined by the geometry of the beam, and the angles p_L, p, and a are either known or can be estimated. It's not entirely clear from your diagram and equations what exactly the angle p represents.

 

[havsula]

You can evaluate what dκ/ds is at the fixed end from the formula above. The variation in EI over the length of the beam is determined by the geometry of the beam, and the angles p_L, p, and a are either known or can be estimated. It's not entirely clear from your diagram and equations what exactly the angle p represents.

I have thought about that, but my problem is that k (curvature) is a part of the differential equation. The only way around that is to chose a EI(s) that to not vary at s=0.
But maybe the shooting method can work for me, since I can guess on a k(0)