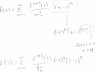SUMMARY
The discussion focuses on finding the Taylor series expansion of the function f(x) = (x-1)/(1+(x-1)^2) about x=1 to compute the 9th and 10th derivatives at that point. The user simplifies the function by substituting u = x - 1, leading to the series representation u/(1+u^2) = u * Σ (-1)^n (u^2)^n. The series converges to Σ (-1)^n (x-1)^(2n+1), allowing for the identification of the 9th and 10th derivatives directly from the series coefficients. The user expresses confusion regarding the derivatives, suspecting an error in their calculations, particularly that they are obtaining zero for both derivatives.
PREREQUISITES
- Understanding of Taylor series and their expansions
- Familiarity with power series and geometric series
- Knowledge of derivatives and their computation
- Ability to manipulate algebraic expressions and series
NEXT STEPS
- Study Taylor series and their applications in calculus
- Learn about power series convergence and manipulation techniques
- Review geometric series and their role in function expansion
- Practice computing higher-order derivatives from series representations
USEFUL FOR
Students and educators in calculus, mathematicians focusing on series expansions, and anyone interested in advanced derivative computations using Taylor series.