DaveC426913
Gold Member
- 24,158
- 8,280
I'm doing some 2D pencil diagrams (CUD - computer-unaided design).
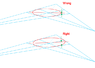
So I've got a square in perspective (2 point perspective but 1 point perspective is good enough). Now I want to draw an ellipse within it, so that the ellipse is properly tangential to all four midpoints of the square. I have an ellipse template to help draw the ellipses.
I know that you can't just align the long axis and short axis of the ellipse to the diagonals of the square (especially since it will be impossible - the square's diagonals are not perpendicular).
I know you have to offset the angle to the ellipse so that it looks right (lies in the same plane as the square).
Is there a formula for what angle one would offset an ellipse's axes to get it to sit right? (A long calculation would not be much good - I'm looking for a shortcut.)
Any takers?
So I've got a square in perspective (2 point perspective but 1 point perspective is good enough). Now I want to draw an ellipse within it, so that the ellipse is properly tangential to all four midpoints of the square. I have an ellipse template to help draw the ellipses.
I know that you can't just align the long axis and short axis of the ellipse to the diagonals of the square (especially since it will be impossible - the square's diagonals are not perpendicular).
I know you have to offset the angle to the ellipse so that it looks right (lies in the same plane as the square).
Is there a formula for what angle one would offset an ellipse's axes to get it to sit right? (A long calculation would not be much good - I'm looking for a shortcut.)
Any takers?
Attachments
Last edited: