Tension and Horizontal Circular Motion

[SeanAmI122886]

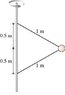
Two wires are tied to the 500 g sphere shown in figure.The sphere revolves in a horizontal circle at a constant speed of 8.40 m/s.

The two wires part of it is throwing me off.
I can do it if it was just one string or two strings if it isn't moving but I am not sure how to do it with circular motion.

Picture of the figure is attached and here is a link if that does not work.

http://session.masteringphysics.com/problemAsset/1000599/6/knight_Figure_07_61.jpg

 

[Astronuc]

Well, one writes a force vector diagram, and then resolves the vectors into horizontal (x or r) and vertical (y) components.

The sphere experiences an outward force, mv²/r and in a gravity field, a downward force mg (its weight).

The wires hold (pull in tension) the sphere to the pole. The tension in each wire acts along the wire, and there are horizontal and vertical components.

The circular motion simply adds a horizontal force to the sphere.

 

[SeanAmI122886]

Wouldn't I have to incorporate the angle of the rope and such.
I don't think I quite grasp what you are saying.

 

[Astronuc]

Wouldn't I have to incorporate the angle of the rope and such.
I don't think I quite grasp what you are saying.

Yes, one must use angles, which can be determined geometrically from the dimensions, then use the appropriate trigonometric function (sin or cos) depending on whether or not the angle is taken with respect to horizontal or vertical, which is the convention.

For instance, the wires form a triangle. Find the angles of the wires with respect to the horizontal. Then the vertical component of tension T is just T sin(theta), and the horiontal component is T cos(theta), where theta is the angle with respect to the horizontal.

Gravity acts in the vertical and the centripetal force is horizontal, in the plane of revolution of the mass.

 

[initialp5]

im having trouble with this same problem...

i don't know what I'm doing wrong...