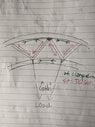
Tension/compression in curved truss? (Diagram attached)

  • Context: Undergrad 
  • Thread starter Thread starter Smilemore
  • Start date Start date
  • Tags Tags
    Truss
Click For Summary
SUMMARY

The discussion centers on the tension and compression forces within a curved truss structure, particularly when subjected to inward loads from cables. The participants highlight that the truss is statically indeterminate, complicating the analysis of stress distribution. A specific scenario is proposed where the central spokes of the truss are uniformly tightened, prompting a discussion on the resulting stress patterns in the truss members, which behave like springs under load.

PREREQUISITES
  • Understanding of statically indeterminate structures
  • Familiarity with truss analysis techniques
  • Knowledge of stress and strain concepts in materials
  • Basic principles of mechanics of materials
NEXT STEPS
  • Research methods for analyzing statically indeterminate structures
  • Study the behavior of truss members under varying loads
  • Learn about the principles of elasticity and material deformation
  • Explore software tools for structural analysis, such as SAP2000 or ANSYS
USEFUL FOR

Structural engineers, civil engineering students, and professionals involved in the design and analysis of truss systems will benefit from this discussion.

Smilemore
Messages
3
Reaction score
1
In the diagram, are the tension/compression labels in the correct position? The curve shown continues into a full circle, with the load pulling inwards from the cables shown
 

Attachments

  • PXL_20220311_092141544.jpg
    PXL_20220311_092141544.jpg
    42.1 KB · Views: 182
Physics news on Phys.org
Smilemore said:
In the diagram, are the tension/compression labels in the correct position? The curve shown continues into a full circle, with the load pulling inwards from the cables shown
Who can say? It is statically indeterminate.

Possibly you want to answer the more specific and difficult question:

"Suppose that the curved truss is put in place with all members relaxed. Now the central spokes are tightened uniformly. What is the resulting pattern of stresses on the truss members now?"
 
Reply
  • Like
Likes   Reactions: Lnewqban
Imagine that each of those elements are springs that can be either compressed (shortening) or tensioned (elongating).
What do you think each will tend to do under the load of those cables?
 

Similar threads

Undergrad Understanding tension and centripedal force in a puck and weight
  • · Replies 4 ·
Replies
4
Views
3K
High School What is tension and how does it affect a rope?
  • · Replies 2 ·
Replies
2
Views
2K
High School Understanding air flow and resistance
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Preloading Pulleys: Understanding the Effects of Tension on Angular Velocity
  • · Replies 3 ·
Replies
3
Views
1K
Undergrad Why are these pulleys equivalent?
  • · Replies 16 ·
Replies
16
Views
2K
What do the numbers in the method of joints analysis for trusses represent?
  • · Replies 3 ·
Replies
3
Views
4K
Undergrad Looking for a trajectory integrator that also supports cubic potential
  • · Replies 6 ·
Replies
6
Views
2K
High School A scenario of non-uniform circular motion
  • · Replies 4 ·
Replies
4
Views
585
Undergrad Tensile and compressive forces
  • · Replies 2 ·
Replies
2
Views
7K
Undergrad Drawbridge falling before caught by rope/cable - Max force
  • · Replies 13 ·
Replies
13
Views
2K