Tension force with pulleys and weights

In summary, the patient with a broken leg is being placed in traction using a special boot with a pulley attached to the sole. The boot, along with the attached mass of 6.0 kg, is suspended by ropes without touching the bed. Using Newton's laws, the tension in the rope was found to be 58.8N. To determine the proper angle for the upper rope, a free-body diagram was used and the angle was found to be 47.58 degrees. To find the net traction force pulling on the leg, the total horizontal force acting on the leg was calculated by adding the horizontal components of the tension in the ropes, resulting in a total of 99.429N.
  • #1
seehuendchen
3
0

Homework Statement



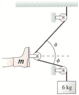
An accident victim with a broken leg is being placed in traction. The patient wears a special boot with a pulley attached to the sole. The foot and boot together have a mass of m = 3.4 kg, and the doctor has decided to hang a 6.0 kg mass from the rope. The boot is held suspended by the ropes and does not touch the bed. ϕ = 10°.

p5-33alt.gif


(a) Determine the amount of tension in the rope by using Newton's laws to analyze the hanging mass.

(b) The net traction force needs to pull straight out on the leg. What is the proper angle θ for the upper rope?

(c) What is the net traction force pulling on the leg? (Hint: If the pulleys are frictionless, which we will assume, the tension in the rope is constant from one end to the other.)

Homework Equations



F=ma
W=mg

The Attempt at a Solution



I was easily able to use W=mg to find the tension in the rope to be 58.8N.
After that, I am lost.

I know the Fnet(y) should be zero since the boot is pulling straight out, but I can't get any further than that...

I also imagine somehow that i will find acceleration along the x-axis, then because the system is in equilibrium (the leg will not move), I will use acceleration and the mass of the boot to find the net traction force.

I really need some help finding the angle theta. Thanks!
 

Attachments

  • p5-33alt.gif
    p5-33alt.gif
    6.7 KB · Views: 1,845
Physics news on Phys.org
  • #2
Okay guys, I started out with a free-body diagram showing the forces on the boot. I found the force of weight on the boot to be 33.32N. I then set fnet(y) equal to zero, which showed that 58.8 sin(theta)=33.2+58.8sin(10) and found the angle to be 47.58 degrees, which was correct.

Now I just can't figure out the third part and have no idea how to go about it. Thanks.
 
  • #3
The new traction will be the total horizontal force acting on the leg, ie the sum of horizontal components of the forces. We already found the angles for the forces to be balanced. Now the total horizontal force will be,

Tcos(10) + Tcos(47.558)

as T = 60N (I take g = 10),

Total HF = 99.429N
 

1. What is tension force in the context of pulleys and weights?

Tension force is a type of force that is exerted by a string, rope, or cable when it is pulled taut. In the context of pulleys and weights, tension force refers to the force that is exerted on the string or cable that runs over the pulley and supports the weight.

2. How does the number of pulleys affect the tension force?

The more pulleys that are used in a system, the more the tension force is distributed across the pulleys. This means that the tension force on each individual pulley will be less than if only one pulley was used. Essentially, the more pulleys, the less tension force is required to lift a weight.

3. Can the direction of tension force change?

Yes, the direction of tension force can change depending on the orientation of the pulleys and the weights. For example, if the pulleys are arranged in a way that the cable runs vertically, the tension force will be directed upwards. However, if the pulleys are arranged in a way that the cable runs horizontally, the tension force will be directed horizontally.

4. How does the weight of the object affect the tension force?

The weight of the object being lifted or pulled by the tension force has a direct impact on the amount of tension force required. The heavier the object, the greater the tension force needed to lift it. This is because the weight of the object exerts a downward force, which must be counteracted by an equal and opposite tension force.

5. What is the relationship between tension force and the number of weights?

The relationship between tension force and the number of weights is directly proportional. This means that as the number of weights increases, the tension force required to lift them will also increase. This is because each weight adds to the overall force that must be counteracted by the tension force.

Similar threads

Leg suspended in a traction system
    • Introductory Physics Homework Help
Replies
18
Views
3K
Newton's Second Law (Pulley Sustem)
    • Introductory Physics Homework Help
Replies
3
Views
783
Monkey accelerating up and down a rope
    • Introductory Physics Homework Help
2
Replies
38
Views
1K
Tension and Angle Analysis for Traction in a Broken Leg
    • Introductory Physics Homework Help
Replies
3
Views
12K
Tension in a complex-pulley-system
    • Introductory Physics Homework Help
Replies
27
Views
1K
System of two pulleys and three masses
    • Introductory Physics Homework Help
Replies
22
Views
3K
Understanding Tension in a Physics Scenario
    • Introductory Physics Homework Help
Replies
9
Views
1K
Solving for Tension in Net Force Equation: Need Help!
    • Introductory Physics Homework Help
Replies
12
Views
1K
Olympiad dynamics problem with 3 masses and a pulley
    • Introductory Physics Homework Help
Replies
17
Views
1K
HW help: Tension/force/acceleration question
    • Introductory Physics Homework Help
Replies
6
Views
2K

Hot Threads

Recent Insights

Back
Top