brotherbobby
- 756
- 170
- Homework Statement
- A rod of length ##L## is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let ##T_1## and ##T_2## be the tensions at the points ##\frac{L}{4}## and ##\frac{3L}{4}## (respectively) away from the pivoted ends. Compare the magnitudes of ##T_1## and ##T_2##.
- Relevant Equations
- Centripetal force needed to keep a particle of ##m## moving in a circle of radius ##r## with angular velocity ##\omega##: ##\;\;\mathbf{F_C = m\omega^2r}##.
(The answer given in the text says ##\boxed{T_1\; >\; T_2}## but, as I show below, I think it's just the opposite).
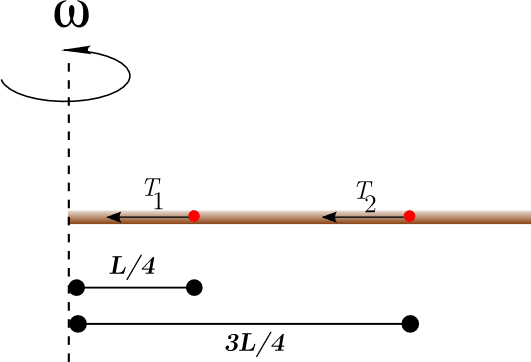
I begin by putting an image relevant to the problem above. Taking a small particle each of the same mass ##m## at the two positions, the centripetal forces are ##T_1 = \frac{m\omega^2 L}{4}## and ##T_2 = \frac{3m\omega^2 L}{4}##.
Clearly, from above, we have ##T_2 > T_1##, contrary to the answer given in the book.
I begin by putting an image relevant to the problem above. Taking a small particle each of the same mass ##m## at the two positions, the centripetal forces are ##T_1 = \frac{m\omega^2 L}{4}## and ##T_2 = \frac{3m\omega^2 L}{4}##.
Clearly, from above, we have ##T_2 > T_1##, contrary to the answer given in the book.