- #1
quietbang
- 4
- 0
Hi, I am currently enrolled in a first year Physics for Scientists and Engineers course at a university, but I am a biochemistry student without a physics background. I am relatively certain that the problem is a forces problem, but there is a chance that it could be energy as we have just begun studying that. I am not sure how to calculate tensions over a non-constant system, particularly if that system is accelerating and not in equilibrium.
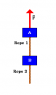
Two 4.56kg blocks connected by a rope are shown.https://loncapa.physics.mcmaster.ca/enc/51/790fe24cb9a36f8b53a9e8421f30c0ad6b5a395de2fa875ae6adf844c8b170def7fe1b61fb49361e0f49fc285eca551db6c419d373e4c41d287a8141ea65c13e.png A second rope hangs beneath the lower block. Both ropes have a mass of 253.0g. The entire assembly is accelerated upward at 3.55m/s2 by force F.
a)What is force F?
b)What is the tension at the top end of rope 1?
c)What is the tension at the bottom end of rope 1?
d)What is the tension at the top end of rope 2?
[itex]
\vec{F}_{net} = \Sigma \vec{F} = m \vec{a}[/itex]
I solved for F by using [itex]\vec{F}_{net_y} = \Sigma \vec{F}_{y_total} = m_{total} \vec{a}_{total}[/itex]
the acceleration of the system is additive, therefore it is
[itex]a= 9.81m/s^2 + 3.55m/s^2[/itex]
[itex]a=13.36m/s^2[/itex]
Total mass of the system is 9.63Kg.
[itex] \vec{F}_{net y} = 9.63kg*13.36m/s^2[/itex]
[itex]F=129N[/itex]
This was the correct answer.
For the next part of the problem, I tried to solve for the bottom of mass A, as that tension would be the same or similar to the tension at the top of the Rope 1.
To do so, I calculated that
[itex] \vec{F}_{net y} = \Sigma \vec{F}_{y} = m_{total} \vec{a}_{total}[/itex]
[itex]\Sigma \vec{F}_{y} = F-T= m_{total} * \vec{a}_{total}[/itex]
[itex]129N-T=m_{total} * \vec{a}_{total}[/itex]
[itex]129N-T=4.56kg*(3.55*9.81)[/itex]
[itex]T=129N*60.9N[/itex]
[itex]T=2.12N[/itex]
This is not the correct answer. I also tried doing it without adding the accelerations and using only the applied acceleration on the system, and got 7.96 N as a result. This is also wrong.
I can't work any further on the problem, as I need this result to calculate the others.
Homework Statement
Two 4.56kg blocks connected by a rope are shown.https://loncapa.physics.mcmaster.ca/enc/51/790fe24cb9a36f8b53a9e8421f30c0ad6b5a395de2fa875ae6adf844c8b170def7fe1b61fb49361e0f49fc285eca551db6c419d373e4c41d287a8141ea65c13e.png A second rope hangs beneath the lower block. Both ropes have a mass of 253.0g. The entire assembly is accelerated upward at 3.55m/s2 by force F.
a)What is force F?
b)What is the tension at the top end of rope 1?
c)What is the tension at the bottom end of rope 1?
d)What is the tension at the top end of rope 2?
Homework Equations
[itex]
\vec{F}_{net} = \Sigma \vec{F} = m \vec{a}[/itex]
The Attempt at a Solution
I solved for F by using [itex]\vec{F}_{net_y} = \Sigma \vec{F}_{y_total} = m_{total} \vec{a}_{total}[/itex]
the acceleration of the system is additive, therefore it is
[itex]a= 9.81m/s^2 + 3.55m/s^2[/itex]
[itex]a=13.36m/s^2[/itex]
Total mass of the system is 9.63Kg.
[itex] \vec{F}_{net y} = 9.63kg*13.36m/s^2[/itex]
[itex]F=129N[/itex]
This was the correct answer.
For the next part of the problem, I tried to solve for the bottom of mass A, as that tension would be the same or similar to the tension at the top of the Rope 1.
To do so, I calculated that
[itex] \vec{F}_{net y} = \Sigma \vec{F}_{y} = m_{total} \vec{a}_{total}[/itex]
[itex]\Sigma \vec{F}_{y} = F-T= m_{total} * \vec{a}_{total}[/itex]
[itex]129N-T=m_{total} * \vec{a}_{total}[/itex]
[itex]129N-T=4.56kg*(3.55*9.81)[/itex]
[itex]T=129N*60.9N[/itex]
[itex]T=2.12N[/itex]
This is not the correct answer. I also tried doing it without adding the accelerations and using only the applied acceleration on the system, and got 7.96 N as a result. This is also wrong.
I can't work any further on the problem, as I need this result to calculate the others.