Tension of Cable Cars in San Francisco's Cable System

[wafflehouse]

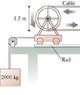
The cable cars in San Francisco are pulled along their tracks by an underground steel cable that moves along at 9.5 mph. The cable is driven by large motors at a central power station and extends, via an intricate pulley arrangement, for several miles beneath the city streets. The length of a cable stretches by up to 100 ft during its lifetime. To keep the tension constant, the cable passes around a 1.5-m-diameter "tensioning pulley" that rolls back and forth on rails, as shown in the figure. A 2000 kg block is attached to the tensioning pulley's cart, via a rope and pulley, and is suspended in a deep hole.

What is the tension in the cable car's cable?

 

[member 553083]

The tension in the cable car's cable is equal to the weight of the block, which is 2000 kg, multiplied by the acceleration due to gravity, which is 9.8 m/s2. Therefore, the tension in the cable car's cable is 19,600 N.