jjiimmyy101
- 74
- 0
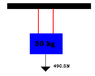
Situation: You have a 50kg box hanging with two different ropes attached to the box at two different points on the box. (The ropes are hanging vertically)
Question: What would be the tension in each rope?
Answer?: Would you just divide the force of the hanging box (490.5N) into two?
I attached a picture.
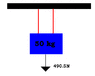
Question: What would be the tension in each rope?
Answer?: Would you just divide the force of the hanging box (490.5N) into two?
I attached a picture.
Attachments
Last edited: