allora_97
- 13
- 0
Tension problem!
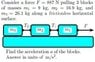
Consider a force F = 887 N pulling 3 blocks
of masses m1 = 9 kg, m2 = 16.9 kg, and
m3 = 26.1 kg along a frictionless horizontal
surface.
The tension of the strings are T1 and T2 (see
sketch).
The equation of motion of m2 is given by
1. T1 − T2 = m1 a .
2. T1 − T2 = m2 a .
3. T1 = m2 a .
4. T1 − T2 = (m1 +m3) a .
5. T1 + T2 = m1 a .
6. T1 = (m1 + m3) a .
7. T1 + T2 = m2 a .
8. T1 = m1 a .
9. T1 + T2 = (m1 +m3) a .
F=ma
T1 = m2a
T2 = m3a
When I try to solve through substitution, I don't get any of the choices above.
What do i do next?
Homework Statement
Consider a force F = 887 N pulling 3 blocks
of masses m1 = 9 kg, m2 = 16.9 kg, and
m3 = 26.1 kg along a frictionless horizontal
surface.
The tension of the strings are T1 and T2 (see
sketch).
The equation of motion of m2 is given by
1. T1 − T2 = m1 a .
2. T1 − T2 = m2 a .
3. T1 = m2 a .
4. T1 − T2 = (m1 +m3) a .
5. T1 + T2 = m1 a .
6. T1 = (m1 + m3) a .
7. T1 + T2 = m2 a .
8. T1 = m1 a .
9. T1 + T2 = (m1 +m3) a .
Homework Equations
F=ma
The Attempt at a Solution
T1 = m2a
T2 = m3a
When I try to solve through substitution, I don't get any of the choices above.
What do i do next?