karter
- 1
- 0
Hi,
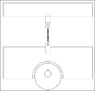
We have been trying to make a machine that tests springs. ( a simple drawing is attached )
We place the spring between two points. The top point has an s-type loadcell attached to get the force data.
The initial size of the spring is 150 mm's. (L0 size)
For the experiment we stretch the spring to 189 mm's and call it L1.
We have an eccentric that is attached to a 5 kw servo motor. It moves the spring up and down 17 mm's each time it rotates.When it rotates the spring is stretched to 206 mm's. (L2)
We continuously get Force data for each rotation. and write it to an excel file.The servo can turn the eccentric 30 times a second.
We have an initial tension (for the aforementioned spring it is 40) and the spring constant is 8.
So according to Hooke's law,
F = IT+k*x we get F = 40+39*8 = 352 N for L1 and for L2 F= 40+56*8 = 488 N I get these results when the machine is not moving.
The problem starts when the servo motor starts running. The servo should run between (1 hz (60 rpm) and 30 hz(1800 rpm)). I can stretch and release the spring 30 times a second. The data we get is not what we expect according to Hooke's law. As the hertz increase the value of F(L2)-F(L1) is getting bigger.
What may be the problem? Is Hooke's law enough for constantly moving springs? Any other forces that may effect the outcome that i overlook?
Thanks in advance.
We have been trying to make a machine that tests springs. ( a simple drawing is attached )
We place the spring between two points. The top point has an s-type loadcell attached to get the force data.
The initial size of the spring is 150 mm's. (L0 size)
For the experiment we stretch the spring to 189 mm's and call it L1.
We have an eccentric that is attached to a 5 kw servo motor. It moves the spring up and down 17 mm's each time it rotates.When it rotates the spring is stretched to 206 mm's. (L2)
We continuously get Force data for each rotation. and write it to an excel file.The servo can turn the eccentric 30 times a second.
We have an initial tension (for the aforementioned spring it is 40) and the spring constant is 8.
So according to Hooke's law,
F = IT+k*x we get F = 40+39*8 = 352 N for L1 and for L2 F= 40+56*8 = 488 N I get these results when the machine is not moving.
The problem starts when the servo motor starts running. The servo should run between (1 hz (60 rpm) and 30 hz(1800 rpm)). I can stretch and release the spring 30 times a second. The data we get is not what we expect according to Hooke's law. As the hertz increase the value of F(L2)-F(L1) is getting bigger.
What may be the problem? Is Hooke's law enough for constantly moving springs? Any other forces that may effect the outcome that i overlook?
Thanks in advance.