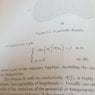Textbook gives the gradient of a scalar as a scalar

[ENgez]

Background: I am currently reading up on homogenization theory.

I have a simple conductivity model (image attached). u is a scalar function (such as potential or temperature).

The textbook proceeds by giving a series expansion for the gradient of u (image attached). the problem is that the gradient is supposed to be a vector function, and the one given is a scalar (pretty sure that the expression given by the book is the differential)

The fact that the gradient is supposedly a scalar makes the divergence operation in the model undefined, which basically makes all following math in the book unclear to me..

How to makes sense of it?

 

[BvU]

Pity we can't read the numbers of the equations; this makes referring to them confusing.

'Thiis series is plugged into the equation' -- study 'the' equation to find out what they mean with $\nabla_y$ and $\nabla _x$ --- my guess is that 's a scalar equation, e.g. for the $z$ component, not a vector equation.

But only a guess, given the little I have to go on.

 

[ENgez]

Thanks, I believe I have found the cause of my confusion.

The model problem is 1-dimensional (x is the only free parameter). This makes the gradient a scalar in the sense that it is a magnitude that can either be positive or negative.
This also makes the divergence and the gradient basically mean the same thing.

This seems to make things work out..